Standard
electroconvection
The classical example of standard EC is observable in
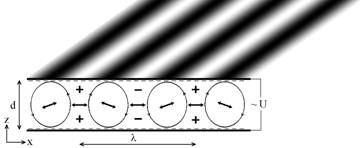
planar cells of a nematic with ea < 0 and sa > 0. The instability occurs due to the Carr-Helfrich feedback mechanism. In the presence of a spatially
periodic director tilt (e.g. a fluctuation) the electric current has a
component normal to the electric field due to the anisotropic electrical
conductivity, which leads to a separation of space charges. The force acting on
these charges in electric field induces a flow forming vortices which exert a
viscous torque on the director closing the feedback loop. If the voltage
exceeds a frequency dependent threshold value, the feedback becomes positive
and a macroscopic pattern develops; otherwise the fluctuations decay.
The precise theoretical description of this mechanism,
known as the standard model of EC, integrates the equations of nematohydrodynamics with Maxwell’s equations assuming an Ohmic electrical conductivity. The equations have two
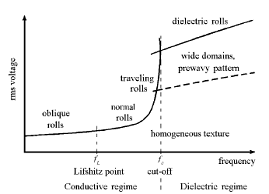
independent solutions corresponding to the conductive and dielectric regimes,
which are characterized by different time symmetries and wave vectors of the
patterns.
|
A sketch of the the
geometry of standard EC. |
Morphological
phase diagram of standard EC. |
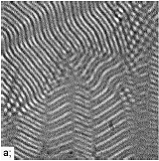
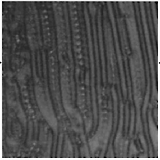
Examples for
standard EC patterns in a planar nematic:
|
Oblique rolls |
|
Dielectric rolls |
Dielectric chevrons |
Standard EC is observable as a primary instability in
planar nematics with ea < 0
and sa > 0
as well as in homeotropic nematics with ea > 0 and sa < 0.
In homeotropic nematics with ea < 0
and sa > 0
as well as in planar nematics with ea > 0 and sa < 0 the primary instability is a homogeneous
deformation (Freedericksz transition) resulting in a
quasi-planar state. Standard EC may then occur at higher voltages as a
secondary bifurcation.
Examples for
standard EC patterns in homeotropic nematics:
|
Disordered oblique
rolls |
Soft squares |
Abnormal rolls |
CRAZY rolls |