Viscous
fingering is a pattern
forming phenomenon in which the interface between two immiscible fluids destabilizes
when the more viscous fluid is displaced by the less viscous one. The use of intrinsically
anisotropic, non-Newtonian,
or complex fluids (e.g., liquid crystals) as a more viscous fluid results in a
much richer morphological diagram than that for isotropic fluids due to shear
thinning/thickening effects, or plastic/elastic effects. Moreover, because of
the dielectric and magnetic anisotropy of the liquid crystals, their relevant
(e.g., viscous, elastic) properties can be easily tuned by electric or magnetic
fields.
Main
results
The influence of
an external electric field on the morphology of the nematic-liquid-crystal–air
interface has been studied in radial Hele-Shaw geometry. The effective
viscosity μeff
of the nematic has been tuned by the electric field E and by the
flow. At low excess pressure pe (where the growth of the
interface is controlled mainly by the surface tension σ), the applied E
has no significant influence on the morphology of the interface, but
decreases its normal velocity due to the increase of μeff. At higher pe
(where the growth is not only controlled by σ, but also by the kinetic
term that depends on the effective viscosity) a significant difference in the
morphology has been observed as a function of E. Experiments have shown
that the influence of the electric field on the pattern morphology increases
with the driving force (pressure gradient).

[Phys. Rev. E 67, 041717/1-7 (2003)] (pdf)
Viscous
fingering of an air-nematic interface in a radial Hele-Shaw cell has been studied
when periodically switching on and off an electric field, which reorients the
nematic and thus changes its viscosity, as well as the surface tension and its
anisotropy (mainly enforced by a single groove in the cell). Undulations at the
sides of the fingers have been observed that correlate with the switching
frequency and with tip oscillations that give maximal velocity to smallest
curvatures. These lateral undulations appear to be decoupled from spontaneous (noise
induced) side branching. It is concluded that the lateral undulations are
generated by successive relaxations between two limiting finger widths. The
change between these two selected pattern scales is mainly due to the change in
the anisotropy. This scenario is confirmed by numerical simulations in the
channel geometry, using a phase-field model for anisotropic viscous fingering.
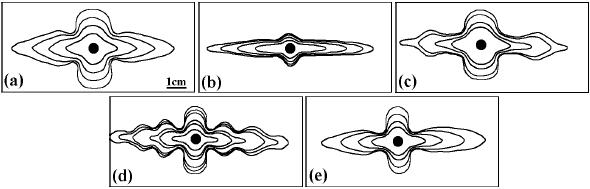
[Phys. Rev. E 64, 056225/1-9 (2001)] (pdf)
The morphological pressure-temperature phase diagram
for viscous fingering patterns observed in the isotropic, nematic and smectic A
phases of the liquid crystal 8CB has been presented. In addition to the dense
branching structure, two distinct dendritic regimes were observed in the
nematic and smectic phases. The dependence of characteristic finger width on
pressure was studied, and the effects of surface and magnetic field alignment
were considered.
[J.
Phys (France) 49, 1319-1323 (1988)]
The Saffman-Taylor instability has been
studied in a Hele-Shaw cell containing nematic liquid crystal 4,
4'-n-octylcyanobiphenyl (8CB). Air injected into the center of the cell gives
rise to viscous fingering patterns, which show a sequence of dense-branching,
dendritic, dense-branching morphologies as a function of temperature. A
qualitative explanation of these morphological transitions is given in terms of
the flow alignment of the director field and the resulting anisotropic viscosity
in the nematic phase of the liquid crystal. The analysis of the fingering
patterns shows that while the perimeter of the pattern is fractal, the pattern
itself is not. The extent to which the pattern is space filling depends on the
morphology and this quantity may serve to indicate the morphological
transitions.

[Phys. Rev. A 36, 3984-3989 (1987)] (pdf)
Experimental data of viscous fingering
patterns have been presented in a radial Hele-Shaw cell filled with the liquid
crystal 8CB. A dense-branching—dendritic-dense-branching morphological phase
sequence has been observed as a function of temperature. The wave number of the
fastest growing mode can be selected by varying experimental parameters, and
the number of initially growing fingers on a circular interface is in good
agreement with linear stability analysis which includes the full kinetic term.
A mechanism is proposed for tip stabilization by anisotropic viscosity; the
critical viscosity ratio for circular tips is ≈2.

[Phys. Rev. A 36, 1527-1529(R)
(1987)] (pdf)
A Hele-Shaw experimental geometry has been introduced
which uses a nematic liquid crystal as the more viscous fluid, so that there is
anisotropy in the medium itself. It has been found that the effective
anisotropy may be tuned by varying the pressure with which the low-viscosity liquid
(air, in this case) enters the cell. As a result re-entrant morphological
transitions have been obtained between random patterns (tip splitting) and
quasi-regular patterns qualitatively resembling dendritic growth (stable tips).