Phase
field group:
Leader: Prof. László
Gránásy (DSc)
Members: Tamás Pusztai (PhD), György Tegze (PhD), Gyula I. Tóth (PhD), László Rátkai (PhD student), Frigyes Podmaniczky (PhD student), Bálint Korbuly (PhD student)
Previous members: László Környei (PhD); Tamás Börzsönyi (PhD), Attila Szállás (PhD)
Latest results:
![[pattern-picture]](crystal_files/image001.jpg) Dendrites
Regularized by Spatially Homogeneous Time-Periodic Forcing
Dendrites
Regularized by Spatially Homogeneous Time-Periodic Forcing
T.
Börzsönyi, T. Tóth-Katona,
Á. Buka, and L. Gránásy
Research
Institute for Solid State Physics and Optics, Hungarian Academy of
Sciences,
P.O.B. 49, H-1525 Budapest, Hungary
The effect of spatially homogeneous
time-periodic
external forcing on dendritic
solidification has been
studied by phase-field modeling and experiments on liquid crystal. It
is shown
that the frequency of dendritic sidebranching
can be tuned by oscillating pressure or heating. The main parameters
that
influence this phenomenon are identified. [Phys.
Rev. Lett. 83, 2853-2856 (1999)].
![[pattern-picture]](crystal_files/image002.gif) Nucleation
and Bulk Crystallization in Binary Phase Field Theory
Nucleation
and Bulk Crystallization in Binary Phase Field Theory
László Gránásy,1
Tamás
Börzsönyi,1,2 and Tamás Pusztai1
1Research Institute for
Solid State Physics and Optics, P.O. Box 49, H-1525 Budapest, Hungary
2Groupe de Physique des Solides, CNRS UMR 75-88,
Universités
Paris VI at VII, Tour 23, 2 place Jussieu, 75251 Paris Cedex 05, France
We present a phase field theory for binary
crystal
nucleation. In the one-component limit, quantitative agreement is
achieved with
computer simulations (Lennard-Jones system)
and
experiments (ice-water system) using model parameters evaluated from
the free
energy and thickness of the interface. The critical undercoolings
predicted for Cu-Ni alloys accord with the measurements, and indicate
homogeneous nucleation. The Kolmogorov
exponents
deduced for dendritic solidification and
for soft impingement of particles via diffusion fields are
consistent
with experiment. [Phys. Rev. Lett. 88,
206105
(2002)].
![[pattern-picture]](crystal_files/image003.gif) Crystal
nucleation and growth in binary phase-field theory
Crystal
nucleation and growth in binary phase-field theory
László Gránásy,1
Tamás
Börzsönyi,1,2 and Tamás Pusztai1
1Research Institute for
Solid State Physics and Optics, POB 49, H-1525 Budapest, Hungary
2Groupe de Physique des Solides, CNRS UMR 75-88,
Universités
Paris VI at VII, Tour 23, 2 place Jussieu,75251, Paris Cedex 05, France
Nucleation and growth in unary and binary systems is investigated in
the
framework of the phase-field theory. Evaluating the model parameters
from the
interfacial free energy and interface thickness, a quantitative
agreement is
found with computer simulations and experiments on the ice water
system. The
critical undercoolings predicted for a
simple binary
system are close to experiment. Phase-field simulations for isotropic
and
anisotropic systems show that due to the interacting diffusion fields
the Avrami Kolmogorov
exponent varies
with transformed fraction and initial concentration. [Journal
of Cryst. Growth, 237-239,
1813 (2002)
![[pattern-picture]](crystal_files/image004.gif) Diffuse
interface analysis of crystal nucleation in hard-sphere liquid
Diffuse
interface analysis of crystal nucleation in hard-sphere liquid
László Gránásy and Tamás Pusztai
Research
Institute for Solid State Physics and Optics, H 1525 Budapest, POB 49,
Hungary
We show that
the
increase of the interface free energy with deviation from equilibrium
seen in
recent Monte Carlo simulations [S. Auer and D. Frenkel,
Nature, London, 413, 711 (2001)] can be recovered if the
molecular
scale diffuseness of the crystal liquid interface is considered. We
compare two
models, Gránásy’s phenomenological diffuse
interface
theory, and a density functional theory that relies on the type of Ginzburg-Landau expansion for fcc nucleation, that
Shih et al. introduced
for bcc crystal. It is shown that, in the range of Monte Carlo
simulations, the
nucleation rate of the stable fcc
phase is by several orders of magnitude higher than for the metastable
bcc phase, seen to nucleate first in other fcc
systems. The nucleation barrier that the diffuse interface theories
predict for
small deviations from equilibrium is in far better agreement with the
simulations than the classical droplet model. The behavior expected at
high
densities is model dependent. Gránásy s
phenomenological diffuse interface theory indicates a spinodal
point close to glass transition, while a nonsingular behavior is
predicted by
the density functional theory with constant Ginzburg-Landau
coefficients. Remarkably, a minimum of the nucleation barrier, similar
to the
one seen in polydisperse systems, occurs
if the known
density dependence of the Ginzburg-Landau
coefficients is considered. [J.
Chem. Phys. B, 117, 10121, (2002)].
![[pattern-picture]](crystal_files/image005.jpg) Phase
Field
Theory of Nucleation and Growth in Binary Alloys
Phase
Field
Theory of Nucleation and Growth in Binary Alloys
László Gránásy,1
Tamás
Börzsönyi,1,2 and Tamás Pusztai1
1Research Institute for
Solid State Physics and Optics, POB 49, H-1525 Budapest, Hungary
2Groupe de Physique des Solides, CNRS UMR 75-88,
Universités Paris
VI at VII, Tour 23, 2 place Jussieu,75251, Paris Cedex 05, France
We present a phase field theory for binary
crystal
nucleation. Using the physical interface thickness, we achieve
quantitative
agreement with computer simulations and experiments for unary and
binary
substances. Large-scale numerical simulations are performed for
multi-particle
freezing in alloys. We deduce the Kolmogorov
exponents for dendritic solidification and
for the
"soft-impingement" of crystallites interacting via diffusion
fields.
[Presented at
International
Workshop on "Computational Physics of Transport and Interface
Dynamics" February18-March 8, 2002. MPIPKS Dresden, Germany; Appeared
in
Interface and Transport Dynamics, edited by H. Emmerich,
B. Nestler and M. Schreckenberg,
Lecture Notes in Computational Science and Engineering, 32,
Springer,
Berlin, (2003) pp 190-195.]
![[pattern-picture]](crystal_files/image006.gif) Growth
of “dizzy dendrites” in a random field of foreign particles
Growth
of “dizzy dendrites” in a random field of foreign particles
László Gránásy,1
Tamás Pusztai,1 James A. Warren,2
Jack F. Douglas,3 Tamás
Börzsönyi,1
and Vincent Ferreiro4
1Research Institute
for Solid State Physics and Optics, PO Box 49, H-1525 Budapest, Hungary
2Metallurgy and 3Polymers Divisions, National
Institute of Standards and Technology, Gaithersburg, Maryland 20899,USA
4Laboratoire de Structure et Properiétés
de l Etat Solide,
CNRS, Batiment C6, 59655 Villeneuve d Ascq,
France
Microstructure plays an essential role in
determining
the properties of crystalline materials. A widely used method to
influence
microstructure is the addition of nucleating agents1. Observations on
films
formed from clay polymer blends indicate that particulate additives, in
addition to serving as nucleating agents, may also perturb crystal
growth, leading
to the formation of irregular dendritic
morphologies.
Here we describe the formation of these dizzy dendrites using a
phase-field
theory, in which randomly distributed foreign particle inclusions
perturb the
crystallization by deflecting the tips of the growing dendrite arms.
This
mechanism of crystallization, which is verified experimentally, leads
to a
polycrystalline structure dependent on particle configuration and
orientation.
Using computer simulations we demonstrate that additives of controlled
crystal
orientation should allow for a substantial manipulation of the
crystallization
morphology. [Nature
Materials, 2, 92 (2003)].
![[pattern-picture]](crystal_files/image007.gif) Phase
field
theory of crystal nucleation in hard sphere liquid
Phase
field
theory of crystal nucleation in hard sphere liquid
László Gránásy,1
Tamás
Pusztai,1 Gyula Tóth,1
Zoltán Jurek,1 Massimo Conti,2
and Bjørn Kvamme3
1Research Institute
for Solid State Physics and Optics, PO Box 49, H-1525 Budapest, Hungary
2Dipartimento di Matematica
e Fisica, Universita
di Camerino,
and Istituto Nazionale
di Fisica della
Materia, Via Madonna delle
Carceri, I-62032, Camerino,
Italy
3University of Bergen, Department of Physics, Allégaten
55, N-5007 Bergen, Norway
The phase field theory
of crystal
nucleation described in L. Gránásy, T. Börzsönyi, and T. Pusztai,
Phys.
Rev. Lett.
88, 206105 (2002) is applied for nucleation in hard-sphere
liquids. The
exact thermodynamics from molecular dynamics is used. The interface
thickness
for phase field is evaluated from the cross-interfacial variation of
the height
of the singlet density peaks. The model parameters are fixed in
equilibrium so
that the free energy and thickness of the (111), (110), and (100)
interfaces
from molecular dynamics are recovered. The density profiles predicted
without adjustable
parameters are in a good agreement with the filtered densities from the
simulations. Assuming spherical symmetry, we evaluate the height of the
nucleation barrier and the Tolman length
without
adjustable parameters. The barrier heights calculated with the
properties of
the (111) and (110) interfaces envelope the Monte Carlo results, while
those
obtained with the average interface properties fall very close to the
exact
values. In contrast, the classical sharp interface model considerably
underestimates
the height of the nucleation barrier. We find that the Tolman
length is positive for small clusters and decreases with increasing
size, a
trend consistent with computer simulations. [Journal of Chemical
Physics, 119, 10376 (2003)].
![[pattern-picture]](crystal_files/image008.jpg) Phase-field
models for eutectic solidification
Phase-field
models for eutectic solidification
Daniel Lewis,1 Tamás Pusztai,2 László Gránásy,2 James A. Warren,1
and
William Boettinger1
1Metallurgy and Polymers Divisions, National
Institute
of Standards and Technology, Gaithersburg, Maryland 20899, USA
2Research Institute for Solid State Physics
and Optics,
PO Box 49, H-1525 Budapest, Hungary
This article discusses two methods for modeling eutectic solidification
using the
phase-field approach. First, a multi-phase-field model is used to study
the
three-dimensional morphological evolution of binary eutectics.
Performing the
calculations in three dimensions allows observation of both lamellar
and
rod-like structures as well as transient phenomena such as lamellar
fault
motion, rod-branching, and nucleation or elimination of phases as
solidification progresses. The second approach models multiple eutectic
grains
where the crystallizing phases have an orientation relationship. This
approach
is promising for modeling complex solidification microstructures. [JOM, 56,
34-39 (2004)].
![[pattern-picture]](crystal_files/image009.jpg) Kinetics
of
solid hydrate formation by carbon dioxide: Phase field theory of
hydrate
nucleation and magnetic resonance imaging
Kinetics
of
solid hydrate formation by carbon dioxide: Phase field theory of
hydrate
nucleation and magnetic resonance imaging
B.
Kvamme,1 A. Graue,1 E. Aspenes,1 T.
Kuynetsova,1 L. Gránásy,2 G. Tóth,2 T.
Pusztai,2 and G. Tegze2
1University of
Bergen, Department of Physics, Allégaten
55, N-5007
Bergen, Norway
2Research Institute for Solid State Physics and Optics,
PO Box
49, H-1525 Budapest, Hungary
In the course of developing a general
kinetic model of
hydrate formation/reaction that can be used to establish/ optimize
technologies
for the exploitation of hydrate reservoirs, two aspects of CO2 hydrate
formation have been studied. (i) We
developed a
phase field theory for describing the nucleation of CO2 hydrate in
aqueous
solutions. The accuracy of the model has been demonstrated on the
hard-sphere
model system, for which all information needed to calculate the height
of the
nucleation barrier is known accurately. It has been shown that the
phase field theory is considerably more accurate than the
sharp-interface
droplet model of the classical nucleation theory. Starting from
realistic
estimates for the thermodynamic and interfacial properties, we have
shown that
under typical conditions of CO2 formation, the size of the
critical fluctuations (nuclei) is comparable to the interface
thickness,
implying that the droplet model should be rather inaccurate. Indeed the
phase
field theory predicts considerably smaller height for the nucleation
barrier
than the classical approach. (ii) In order to provide accurate
transformation
rates to test the kinetic model under development, we applied magnetic
resonance imaging to monitor hydrate phase transitions in porous media
under
realistic conditions. The mechanism of natural gas hydrate conversion
to
CO2-hydrate implies storage potential for CO2 in natural gas hydrate
reservoirs,
with the additional benefit of methane production. We present the
transformation rates for the relevant processes (hydrate formation,
dissociation and recovery). [Phys.
Chem. Chem. Phys., 6, 2327-2334
(2004)].
![[pattern-picture]](crystal_files/image010.jpg) A
general
mechanism for polycrystalline growth
A
general
mechanism for polycrystalline growth
László Gránásy,1
Tamás
Pusztai,1 Tamás Börzsönyi,1
James A. Warren2 and Jack F. Douglas3
1Research Institute
for Solid State Physics and Optics, PO Box 49, H-1525 Budapest, Hungary
2Metallurgy and 3Polymers Divisions, National
Institute of Standards and Technology, Gaithersburg, Maryland 20899,USA
Most research into microstructure formation
during
solidification has focused on single-crystal growth ranging from
faceted
crystals to symmetric dendrites. However, these growth forms can be
perturbed
by heterogeneities, yielding a rich variety of polycrystalline growth
patterns.
Phase-field simulations show that the presence of particulates (for
example,
dirt) or a small rotational translational mobility ratio
(characteristic of
high supercooling) in crystallizing fluids
give rise
to similar growth patterns, implying a duality in the growth process in
these
structurally heterogeneous fluids. Similar crystallization patterns are
also
found in thin polymer films with particulate additives and pure films
with high
supercooling. This duality between the
static and
dynamic heterogeneity explains the ubiquity of polycrystalline growth
patterns
in polymeric and other complex fluids. [Nature
Materials, 3, 645 (2004)].
![[pattern-picture]](crystal_files/image011.jpg) Nucleation
and polycrystalline formation in binary phase field theory
Nucleation
and polycrystalline formation in binary phase field theory
László Gránásy,1
Tamás
Pusztai,1 Tamás Börzsönyi,1
James A. Warren,2 Bjørn Kvamme,3
and P.F. James4
1Research Institute
for Solid State Physics and Optics, PO Box 49, H-1525 Budapest, Hungary
2Metallurgy Division, National Institute of Standards and
Technology, Gaithersburg, Maryland 20899,USA
3University of Bergen, Department of Physics, Allégaten
55, N-5007 Bergen, Norway
4Glass Research Centre, Department of Engineering
Materials, The
University of Sheffield, Sir Robert Hadfield
Building, Mappin Street, Sheffield S1 3JD,
UK
We present a phase field theory for the
nucleation and
growth of one and two phase crystals solidifying with different
crystallographic orientations in binary alloys. The accuracy of the
model is
tested for crystal nucleation in single component systems. It is shown
that
without adjustable parameters the height of the nucleation barrier is
predicted
with reasonable accuracy. The kinetics of primary solidification is
investigated as a function of model parameters under equiaxial
conditions. Finally, we study the formation of polycrystalline growth
morphologies (disordered dendrites, spherulites
and
fractal-like aggregates). [Phys.
Chem. Glass, 45, 107-115 (2004)].
We
thank V. Ferreiro and J. F. Douglas for
the
experimental images (darker pictures).
![[pattern-picture]](crystal_files/image012.jpg) Modelling polycrystalline
solidification using
phase field theory
Modelling polycrystalline
solidification using
phase field theory
László Gránásy,1
Tamás Pusztai,1 and James A.
Warren,2
1Research Institute for Solid State Physics
and Optics,
PO Box 49, H-1525 Budapest, Hungary
2Metallurgy Division, National Institute of Standards and
Technology, Gaithersburg, Maryland 20899,USA
We
review recent advances made in the phase field modelling
of polycrystalline solidification. Areas covered include the
development of
theory from early approaches that allow for only a few crystal
orientations, to
the latest models relying on a continuous orientation field and a free
energy
functional that is invariant to the rotation of the laboratory frame.
We
discuss a variety of phenomena, including homogeneous nucleation and
competitive growth of crystalline particles having different crystal
orientations, the kinetics of crystallization, grain boundary dynamics,
and the
formation of complex polycrystalline growth morphologies including
disordered
(dizzy) dendrites, spherulites,
fractal-like polycrystalline
aggregates, etc. Finally, we extend the approach by incorporating
walls, and
explore phenomena such as heterogeneous nucleation, particle front
interaction,
and solidification in confined geometries (in channels or porous
media). [J.Phys.
Condens. Matter 16, R1205 (2004)]
![[pattern-picture]](crystal_files/image013.gif) Multiphase
solidification in multicomponent alloys
Multiphase
solidification in multicomponent alloys
U. Hecht,1
L.
Gránásy,2 T. Pusztai,2 B. Böttger,1 M.
Apel,1
V. Witusiewicz,1 L. Ratke,3 J. De Wilde,4
L.
Froyen,4 D. Camel,5 B. Drevet,5 G.
Faivre,6
S.G. Fries,1 B. Legendre,7 and S. Rex1
1ACCESS e.V, Aachen, Germany
2Research Institute for Solid State Physics and Optics of
the
Hungarian Academy of Sciences, Budapest, Hungary
3Institute of Space Simulation DLR Köln, Germany
4Departement MTM, Katholieke Universiteit Leuven,
Faculteit Toegepaste
Wetenschappen, Leuven,
Belgium
5CEA-Grenoble, Grenoble, France
6Groupe de Physique des Solides
(GPS), Université Paris 6, Paris, France
7Laboratoire de Chimie Physique
Minérale et Bioinorganique,
EA
401, Faculté de Pharmacie,
Chatenay-Malabry, France
Multiphase solidification in multicomponent
alloys is pertinent to many commercial materials and industrial
processes,
while also raising challenging questions from a fundamental point of
view.
Within the past few years, research activities dedicated to multiphase
solidification of ternary and multicomponent
alloys
experienced considerable amplification. This paper gives an overview of
our
present understanding in this field and the experimental techniques and
theoretical methods research relies on. We start with an introduction
to
thermodynamic databases and computations and emphasize the importance
of thermophysical property data. Then, we
address pattern
formation during coupled growth in ternary alloys and cover
microstructure
evolution during successive steps of phase formation in solidifying multicomponent alloys. Subsequently, we review
advances
made in phase field modeling of multiphase solidification in binary and
multicomponent alloys, including various
approaches to
crystal nucleation and growth. Concluding, we address open questions
and
outline future prospects on the basis of a close interaction among
scientists
investigating the thermodynamic, thermophysical
and microstructural properties of these
alloys. [Materials
Science and
Engineering R 46, 1 (2004)]
![[pattern-picture]](crystal_files/image014.jpg) Nucleation
and the solid-liquid free energy
Nucleation
and the solid-liquid free energy
David
T. Wu,1 László
Gránásy,2 and Frans Spaepen3
This article reviews the current
understanding of the
fundamentals of nucleation theory and its use to extract values for the
solid liquid
interfacial free energy from experimental and simulation data. [MRS Bulletin,
December 2004]
![[pattern-picture]](crystal_files/image015.gif) Growth
and
form of spherulites
Growth
and
form of spherulites
L.
Gránásy,1 T. Pusztai,1
G. Tegze,1
J.A. Warren2 and J.F. Douglas3
1Research Institute
for Solid State Physics and Optics, PO Box 49, H-1525 Budapest, Hungary
2Metallurgy and 3Polymers Divisions, National
Institute of Standards and Technology, Gaithersburg, Maryland 20899,USA
Many structural materials (metal alloys,
polymers,
minerals, etc.) are formed by quenching liquids into crystalline
solids.
This highly nonequilibrium process often
leads to
polycrystalline growth patterns that are broadly termed "spherulites" because of their large-scale
average
spherical shape. Despite the prevalence and practical importance of spherulite formation, only rather qualitative
concepts of
this phenomenon exist. It is established that phase field methods
naturally
account for diffusional instabilities that
are
responsible for dendritic single-crystal
growth. However,
a generalization of this model is required to describe spherulitic
growth patterns, and in the present paper we propose a minimal model of
this
fundamental crystal growth process. Our calculations indicate that the
diversity of spherulitic growth
morphologies arises
from a competition between the ordering effect of discrete local
crystallographic symmetries and the randomization of the local
crystallographic
orientation that accompanies crystal grain nucleation at the growth
front growth front nucleation
(GFN). This
randomization in the orientation accounts for the isotropy of spherulitic growth at large length scales and
long times.
In practice, many mechanisms can give rise to GFN, and the present work
describes and explores three physically prevalent sources of disorder
that lead
to this kind of growth. While previous phase field modeling elucidated
two of
these mechanisms - disorder created by particulate impurities or other
static
disorder or by the dynamic heterogeneities that spontaneously form in supercooled liquids (even pure ones)
- the
present paper considers an additional mechanism, crystalline branching
induced
by a misorientation-dependent grain
boundary energy,
which can significantly affect spherulite
morphology.
We find the entire range of observed spherulite
morphologies can be reproduced by this generalized phase field model of
polycrystalline growth. [Phys.
Rev. E 72, 011605 (2005)]
![[pattern-picture]](crystal_files/image016.gif) Phase
field theory of polycrystalline solidification in three dimensions
Phase
field theory of polycrystalline solidification in three dimensions
T.
Pusztai, G. Bortel
and L. Gránásy
Research
Institute for Solid State Physics and Optics H-1525 Budapest, POB 49,
Hungary
A phase field theory of polycrystalline
solidification
is presented that describes the nucleation and growth of anisotropic
particles
with different crystallographic orientation in 3D dimensions. As
opposed with
the two-dimensional case, where a single orientation field suffices, in
three
dimensions, minimum three fields are needed. The free energy of grain
boundaries is assumed to be proportional to the angular difference
between the
adjacent crystals expressed here in terms of the differences of the
four
symmetric Euler parameters. The equations of motion for these fields
are
obtained from variational principles.
Illustrative
calculations are performed for polycrystalline solidification with dendritic, needle and spherulitic
growth morphologies. [Europhys. Lett. 71, 131 (2005)]
![[pattern-picture]](crystal_files/image017.jpg) Phase
field
modeling of polycrystalline freezing
Phase
field
modeling of polycrystalline freezing
T.
Pusztai, G. Bortel
and
L. Gránásy
Research
Institute for Solid State Physics and Optics, PO Box 49, H-1525
Budapest,
Hungary
The formation of two and three-dimensional
polycrystalline structures are addressed within the framework of the
phase
field theory. While in two dimensions a single orientation angle
suffices to
describe crystallographic orientation in the laboratory frame, in three
dimensions, we use the four symmetric Euler parameters to define
crystallographic orientation. Illustrative simulations are performed
for
various polycrystalline structures including simultaneous growth of
randomly oriented
dendritic particles, the formation of spherulites and crystal sheaves. [Materials Science
and
Engineering A 413–414, 412–417
(2005)]
![[pattern-picture]](crystal_files/image018.gif) Phase
field
simulation of liquid phase separation with fluid flow
Phase
field
simulation of liquid phase separation with fluid flow
G.
Tegze, T. Pusztai
and L. Gránásy
Research
Institute for Solid State Physics and Optics, PO Box 49, H-1525
Budapest,
Hungary
A phase-field theory of binary liquid phase
separation
coupled to fluid flow is presented. The respective Cahn–Hilliard-type
and Navier–Stokes equations are solved
numerically.
We incorporate composition and temperature dependent capillary forces.
The free
energies of the bulk liquid phases are taken from the regular solution
model.
In the simulations, we observe Marangoni
motion, and
direct and indirect hydrodynamic interactions between the droplets. We
find
that coagulation is dramatically accelerated by flow effects. Possible
extension of the model to solidification is discussed.
Video
[Materials Science
and
Engineering A 413–414, 418–422
(2005)]
![[pattern-picture]](crystal_files/image020.jpg) Phase
field
theory of crystal nucleation and polycrystalline growth: A review
Phase
field
theory of crystal nucleation and polycrystalline growth: A review
L. Gránásy,1 T. Pusztai,1 T.
Börzsönyi,1
G. Tóth,1 G. Tegze,1 J.A. Warren,2 and
J.F.
Douglas2
1Research Institute
for Solid State Physics and Optics, H-1525 Budapest, Hungary
2National Institute of Standards and
Technology,
Gaithersburg, Maryland 20899
We
briefly review our recent modeling of crystal nucleation and
polycrystalline
growth using a phase field theory. First, we consider the applicability
of
phase field theory for describing crystal nucleation in a model hard
sphere
fluid. It is shown that the phase field theory accurately predicts the
nucleation
barrier height for this liquid when the model parameters are fixed by
independent molecular dynamics calculations. We then address various
aspects of
polycrystalline solidification and associated crystal pattern formation
at
relatively long timescales. This late stage growth regime, which is not
accessible by molecular dynamics, involves nucleation at the growth
front to
create new crystal grains in addition to the effects of primary
nucleation.
Finally, we consider the limit of extreme polycrystalline growth, where
the
disordering effect due to prolific grain formation leads to isotropic
growth
patterns at long times, i.e., spherulite
formation. Our model of spherulite
growth exhibits
branching at fixed grain misorientations,
induced by
the inclusion of a metastable minimum in
the orientational free energy. It
is demonstrated that a
broad variety of spherulitic patterns can
be
recovered by changing only a few model parameters. [J. Mater. Res., 21, 309 (2006)]
![[pattern-picture]](crystal_files/image021.jpg) Multiscale approach to CO2 hydrate
formation in
aqueous solution: Phase field theory and molecular dynamics. Nucleation
and
growth
Multiscale approach to CO2 hydrate
formation in
aqueous solution: Phase field theory and molecular dynamics. Nucleation
and
growth
György Tegze,1 Tamás
Pusztai,1 Gyula Tóth,1
László Gránásy,1 Atle
Svandal,2 Trygve Buanes,2
Tatyana Kuznetsova,2 and Bjørn
Kvamme2
1Research Institute for Solid State Physics
and Optics,
P.O. Box 49, H-1525 Budapest, Hungary
2Institute of Physics and Technology, University of
Bergen, Allégaten 55, N-5007 Bergen, Norway
A
phase field theory with model parameters evaluated from atomistic
simulations/experiments is applied to predict the nucleation and growth
rates
of solid CO2 hydrate in aqueous solutions under conditions typical to
underwater natural gas hydrate reservoirs. It is shown that under
practical
conditions a homogeneous nucleation of the hydrate phase can be ruled
out. The
growth rate of CO2 hydrate dendrites has been determined from phase
field
simulations as a function of composition while using a physical
interface
thickness 0.85±0.07 nm evaluated from molecular
dynamics
simulations. The growth rate extrapolated to realistic supersaturations
is about three orders of magnitude larger than the respective
experimental
observation. A possible origin of the discrepancy is discussed. It is
suggested
that a kinetic barrier reflecting the difficulties in building the
complex
crystal structure is the most probable source of the deviations. [J. Chem. Phys. 124,
234710 (2006)]
![[pattern-picture]](crystal_files/image022.jpg) Phase
field
theory of polycrystalline freezing in three dimensions
Phase
field
theory of polycrystalline freezing in three dimensions
Tamás
Pusztai, Gábor
Bortel and László
Gránásy
Research
Institute for Solid State Physics and Optics; H-1525 Budapest, POB 49,
Hungary
A phase field theory, we proposed recently
to describe
nucleation and growth in three dimensions (3D), has been used to study
the
formation of polycrystalline patterns in the alloy systems Al-Ti and
Cu-Ni. In
our model, the free energy of grain boundaries is assumed proportional
to the
angular difference between the adjacent crystals expressed in terms of
the
differences of the four symmetric Euler parameters called quaternions.
The equations of motion for these fields have been obtained from variational principles. In the simulations cubic
crystal
symmetries are considered. We investigate the evolution of polydendritic
morphology, present simulated analogies of the metallographic images,
and
explore the possibility of modeling solidification in thin layers.
Transformation kinetics in the bulk and in thin films is discussed in
terms of
the Johnson-Mehl-Avrami-Kolmogorov
approach. [Modeling
of Casting,
Welding and Advanced Solidification Processes- XI, TMS 409 (2006)]
![[pattern-picture]](crystal_files/image023.jpg) Phase
field
theory of liquid phase separation and solidification with melt flow
Phase
field
theory of liquid phase separation and solidification with melt flow
György Tegze and
László Gránásy
Research
Institute for
Solid State Physics and Optics; H-1525 Budapest, POB 49, Hungary
A
phase-field theory of binary liquid phase separation and solidification
coupled
to fluid flow is presented. The respective equations of motion and Navier-Stokes equations are solved numerically.
We
incorporate composition and temperature dependent capillary forces. The
free
energies of the bulk liquid phases are taken from the regular solution
model.
In the simulations, we observe Marangoni
motion of
the droplets, and direct and indirect hydrodynamic interactions between
the
droplets. We observe that capillary effects dramatically accelerate
droplet
coagulation and that solidification interacts with liquid phase
separation. [Modeling
of Casting, Welding and Advanced Solidification Processes- XI, TMS 513
(2006)]
![[pattern-picture]](crystal_files/image024.jpg) Polycrystalline
patterns in far-from-equilibrium freezing: a phase field study
Polycrystalline
patterns in far-from-equilibrium freezing: a phase field study
L. Gránásy,1
T.
Pusztai,1 T. Börzsönyi,1 G. Tóth,1 G.
Tegze,1
J.A. Warren,2 and J.F. Douglas2
1Research Institute for Solid State Physics and Optics,
H-1525
Budapest, Hungary
2National Institute of Standards and Technology,
Gaithersburg,
Maryland 20899
We discuss the formation of polycrystalline
microstructures within the framework of phase field theory. First, the
model is
tested for crystal nucleation in a hard sphere system. It is shown
that, when
evaluating the model parameters from molecular dynamics simulations,
the phase
field theory predicts the nucleation barrier for hard spheres
accurately. The
formation of spherulites is described by
an extension
of the model that incorporates branching with a definite orientational
mismatch. This effect is induced by a metastable
minimum in the orientational free energy. Spherulites are an extreme example of
polycrystalline
growth, a phenomenon that results from the quenching of orientational
defects (grain boundaries) into the solid as the ratio of the
rotational to the
translational diffusion coefficient is reduced, as is found at high undercoolings. It is demonstrated that a broad
variety of spherulitic patterns can be
recovered by changing only a
few model parameters. [Philos.
Mag. 86 3757 (2006)]
![[pattern-picture]](crystal_files/image025.jpg) Phase
field
theory of nucleation and polycrystalline pattern formation
Phase
field
theory of nucleation and polycrystalline pattern formation
L. Gránásy,
T. Pusztai and T. Börzsönyi
Research
Institute for
Solid State Physics and Optics, H-1525 Budapest, Hungary
We
review our recent modeling of crystal nucleation and polycrystalline
growth
using a phase field theory. First, we consider the applicability of
phase field
theory for describing crystal nucleation in a model hard sphere fluid.
It is
shown that the phase field theory accurately predicts the nucleation
barrier
height for this liquid when the model parameters are fixed by
independent molecular
dynamics calculations. We then address various aspects of
polycrystalline
solidification and associated crystal pattern formation at relatively
long
timescales. This late stage growth regime, which is not accessible by
molecular
dynamics, involves nucleation at the growth front to create new crystal
grains
in addition to the effects of primary nucleation. Finally, we consider
the
limit of extreme polycrystalline growth, where the disordering effect
due to
prolific grain formation leads to isotropic growth patterns at long
times,
i.e., spherulite formation. Our
model of spherulite growth exhibits
branching at
fixed grain misorientations, induced by
the inclusion
of a metastable minimum in the orientational
free energy. It is demonstrated that a broad variety of spherulitic patterns can be recovered by
changing only a
few model parameters. [Handbook
of Theoretical and Computational Nanotechnology, Edited by Michael Rieth and Wolfram Schommers
American Scientific Publishers, Stevenson Ranch, CAL, 2006, Volume 9:
Pages (525-572)]
![[pattern-picture]](crystal_files/image026.jpg) Phase
field
theory of heterogeneous crystal nucleation
Phase
field
theory of heterogeneous crystal nucleation
L. Gránásy,1 T. Pusztai,1 D. Saylor,2
and J.A. Warren3
1Research Institute for Solid State Physics and Optics,
H-1525
Budapest, Hungary
2Food and Drug Administration, Rockville,
Maryland
20852, USA
3National Institute of Standards and Technology,
Gaithersburg,
Maryland 20899, USA
The phase field approach is used to model
heterogeneous crystal nucleation in an undercooled
pure liquid in contact with a foreign wall. We discuss various choices
for the
boundary condition at the wall and determine the properties of critical
nuclei,
including their free energy of formation and the contact angle as a
function of
undercooling. For particular choices of
boundary
conditions, we may realize either an analog of the classical spherical
cap
model or decidedly nonclassical behavior,
where the
contact angle decreases from its value taken at the melting point
towards
complete wetting at a critical undercooling,
an
analogue of the surface spinodal of
liquid-wall
interfaces. [Phys.
Rev. Lett. 98, 035703 (2007) ]
![[pattern-picture]](crystal_files/image027.jpg) Phase
field
theory of interfaces and crystal nucleation in a eutectic system of fcc structure: I.
Transitions in
the one-phase liquid region
Phase
field
theory of interfaces and crystal nucleation in a eutectic system of fcc structure: I.
Transitions in
the one-phase liquid region
Gy.
I. Tóth and L. Gránásy,
Research
Institute for
Solid State Physics and Optics, H-1525 Budapest, Hungary
The
phase field theory PFT has been applied to predict equilibrium
interfacial
properties and nucleation barrier in the binary eutectic system Ag–Cu
using
double well and interpolation functions deduced from a Ginzburg-Landau
expansion that considers fcc
face centered cubic crystal symmetries. The temperature and composition
dependent free energies of the liquid and solid phases are taken from
Calculation of Phase Diagrams-type calculations. The model parameters
of PFT
are fixed so as to recover an interface thickness of 1 nm from
molecular
dynamics simulations and the interfacial free energies from the
experimental
dihedral angles available for the pure components. A nontrivial
temperature and
composition dependence for the equilibrium interfacial free energy is
observed.
Mapping the possible nucleation pathways, we find that the Ag and Cu
rich
critical fluctuations compete against each other in the neighborhood of
the
eutectic composition. The Tolman length is
positive
and shows a maximum as a function of undercooling.
The PFT predictions for the critical undercooling
are
found to be consistent with experimental results. These results support
the
view that heterogeneous nucleation took place in the undercooling
experiments available at present. We also present calculations using
the
classical droplet model classical nucleation theory CNT and a
phenomenological
diffuse interface theory DIT. While the predictions of the CNT with a
purely
entropic interfacial free energy underestimate the critical undercooling,
the DIT results appear to be in a reasonable agreement with the PFT
predictions. [J.
Chem. Phys. 127, 074709 (2007)]
![[pattern-picture]](crystal_files/image028.jpg) Phase
field
theory of interfaces and crystal nucleation in a eutectic system of fcc structure: II.
Nucleation in
the metastable liquid immiscibility region
Phase
field
theory of interfaces and crystal nucleation in a eutectic system of fcc structure: II.
Nucleation in
the metastable liquid immiscibility region
G. I. Tóth
and L. Gránásy,
Research
Institute for
Solid State Physics and Optics, H-1525 Budapest, Hungary
In
the second part of our paper, we address crystal nucleation in the metastable liquid miscibility region of eutectic
systems
that is always present, though experimentally often inaccessible. While
this
situation resembles the one seen in single component crystal nucleation
in the
presence of a metastable vapor-liquid
critical point
addressed in previous works, it is more complex because of the fact
that here
two crystal phases of significantly different compositions may
nucleate.
Accordingly, at a fixed temperature below the critical point, six
different
types of nuclei may form: two liquid-liquid nuclei: two solid-liquid
nuclei;
and two types of composite nuclei, in which the crystalline core has a
liquid
“skirt,” whose composition falls in between the compositions of the
solid and
the initial liquid phases, in addition to nuclei with concentric
alternating
composition shells of prohibitively high free energy. We discuss
crystalline
phase selection via exploring/identifying the possible pathways for
crystal
nucleation. [J.
Chem. Phys. 127, 074710 (2007)]
 Phase-field approach to polycrystalline
solidification including
heterogeneous and homogeneous nucleation.
Phase-field approach to polycrystalline
solidification including
heterogeneous and homogeneous nucleation.
T. Pusztai,1
G.
Tegze,2 G. I. Tóth,1 L. Környei,1 G.
Bansel,2
Z. Fan,2 and L. Gránásy2
1Research Institute for Solid State Physics and Optics,
H-1525
Budapest, Hungary;
2Brunel Centre for Advanced Solidification Technology, Brunel University, Uxbridge UB8 3PH, UK
Advanced
phase-field techniques have been applied to address various aspects of
polycrystalline solidification including different modes of crystal
nucleation.
The height of the nucleation barrier has been determined by solving the
appropriate Euler-Lagrange equations. The examples shown include the
comparison
of various models of homogeneous crystal nucleation with atomistic
simulations
for the single-component hard sphere fluid. Extending previous work for
pure
systems [Gránásy et al., Phys. Rev.
Lett. 98, 035703 (2007)],
heterogeneous nucleation
in unary and binary systems is described via introducing boundary
conditions
that realize the desired contact angle. A
quaternion
representation of crystallographic orientation of the individual
particles
[outlined in Pusztai et al., Europhys. Lett. 71,
131 (2005)] has been applied for modeling a
broad variety of polycrystalline structures including crystal sheaves, spherulites and those built of crystals with dendritic, cubic, rhombo-dodecahedral
and truncated octahedral growth morphologies. Finally, we present
illustrative
results for dendritic polycrystalline
solidification
obtained using an atomistic phase-feld
model. [J.
Phys.: Condens. Matter 20,
404205 (2008)]
Advanced operator-splitting-based semi-implicit spectral
method to
solve the binary phase-field crystal equation with variable
coefficients.

G. Tegze,1
G. Bansel,1 G. I. Tóth,2 T. Pusztai,2
Z. Fan,1
and L. Gránásy1
1Brunel Centre for Advanced Solidification
Technology, Brunel University, Uxbridge
UB8 3PH, UK
2Research Institute for Solid State Physics and Optics,
H-1525
Budapest, Hungary
We
present an efficient method to solve numerically the equations of
dissipative
dynamics of the binary phase-field crystal model proposed by Elder et
al. [K.R.
Elder, M. Katakowski, M. Haataja,
M. Grant, Phys. Rev. B 75, 064107 (2007)] characterized by variable
coefficients. Using the operator splitting method, the problem has been
decomposed into sub-problems that can be solved more efficiently. A
combination
of non-trivial splitting with spectral semi-implicit solution leads to
sets of
algebraic equations of diagonal matrix form. Extensive testing of the
method
has been carried out to find the optimum balance among errors
associated with
time integration, spatial discretization,
and
splitting. We show that our method speeds up the computations by orders
of
magnitude relative to the conventional explicit finite difference
scheme, while
the costs of the pointwise implicit
solution per timestep remains low. Also we
show that due to its
numerical dissipation, finite differencing can not compete with
spectral
differencing in terms of accuracy. In addition, we demonstrate that our
method
can efficiently be parallelized for distributed memory systems, where
an
excellent scalability with the number of CPUs is observed. [J. Comput. Phys. 228, 1612 (2009)]
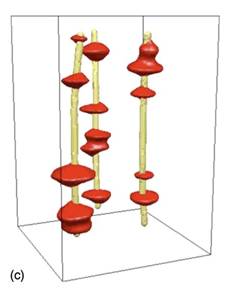 Phase
field approach to heterogeneous nucleation in alloys.
Phase
field approach to heterogeneous nucleation in alloys.
J. A. Warren,1
T. Pusztai,2 L. Környei,2 and L. Gránásy3
1Metallurgy Division, National Institute of Standards and
Technology, Gaithersburg, Maryland 20899, USA
2Research Institute for Solid State Physics and Optics,
H-1525
Budapest, Hungary
3 Brunel Centre for Advanced
Solidification Technology, Brunel
University,
Uxbridge UB8 3PH, UK
We
extend the phase field model of heterogeneous crystal nucleation
developed
recently [L. Gránásy et al., Phys.
Rev. Lett. 98, 035703 (2007)] to
binary alloys. Three
approaches are considered to incorporate foreign walls of tunable
wetting
properties into phase field simulations: a continuum realization of the
classical spherical cap model (called model A herein), a nonclassical
approach (model B) that leads to ordering of the liquid at the wall and
to the
appearance of a surface spinodal, and a nonclassical model (model C) that allows for the
appearance
of local states at the wall that are accessible in the bulk phases only
via
thermal fluctuations. We illustrate the potential of the presented
phase field
methods for describing complex polycrystalline solidification
morphologies
including the shish-kebab structure, columnar to equiaxed
transition, and front-particle interaction in binary alloys. [Phys.
Rev. B
79, 014204 (2009)]
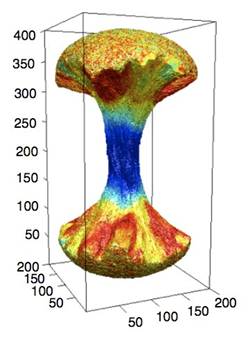
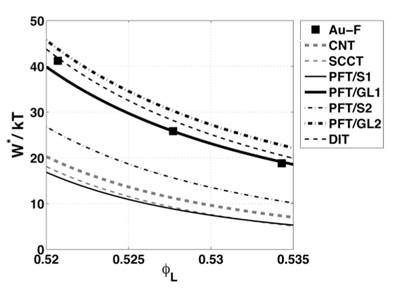 Crystal
nucleation in the hard-sphere system revisited: A critical test of
theoretical
approaches
Crystal
nucleation in the hard-sphere system revisited: A critical test of
theoretical
approaches
G. I. Tóth1
and
L. Gránásy2
1Research Institute for Solid State Physics
and Optics,
H-1525 Budapest, Hungary
2Brunel Centre for Advanced Solidification Technology, Brunel University, Uxbridge UB8 3PH, UK
The
hard-sphere system is the best known fluid that crystallizes: the
solid-liquid
interfacial free energy, the equations of state, and the height of the
nucleation barrier are known accurately, offering a unique possibility
for a
quantitative validation of nucleation theories. A recent significant
downward
revision of the interfacial free energy from 0.61kT/s2 to 0.56 kT/s2 [Davidchack,
R.; Morris, J. R.; Laird, B. B. J. Chem.
Phys. 125, 094710 (2006)] necessitates a re-evaluation of
theoretical approaches to crystal nucleation. This has been carried out
for the
droplet model of the classical nucleation theory (CNT), the
self-consistent
classical theory (SCCT), a phenomenological diffuse interface theory
(DIT), and
single- and two-field variants of the phase field theory that rely on
either
the usual double-well and interpolation functions (PFT/S1 and PFT/S2,
respectively) or on a Ginzburg-Landau
expanded free
energy that reflects the crystal symmetries (PFT/GL1 and PFT/GL2). We
find that
the PFT/GL1, PFT/GL2, and DIT models predict fairly accurately the
height of
the nucleation barrier known from Monte Carlo simulations in the volume
fraction range of 0.52 < f < 0.54, whereas the CNT, SCCT, PFT/S1,
and PFT/S2
models underestimate it significantly. [J.
Phys. Chem.
B 113, 5141 (2009)]
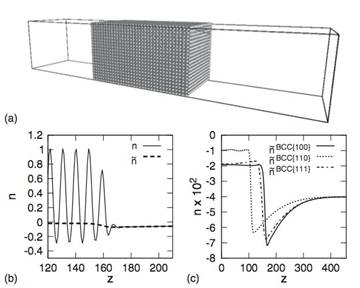 Diffusion-controlled
anisotropic growth of stable and metastable
crystal
polymorphs in the phase-field crystal model
Diffusion-controlled
anisotropic growth of stable and metastable
crystal
polymorphs in the phase-field crystal model
G. Tegze,1
L.
Gránásy,1 G. I. Tóth,2 F. Podmaniczky,2
A.
Jaatinen,3 T. Ala-Nissila,3 and
T. Pusztai2
1Brunel Centre for Advanced Solidification Technology, Brunel University, Uxbridge UB8 3PH, UK
2Research Institute for Solid State Physics and Optics,
H-1525
Budapest, Hungary
3Department of Applied Physics, Helsinki University of
Technology,
Post Office Box 1100, FI-02015 TKK, Finland
We
use a simple density functional approach on a diffusional
time scale, to address freezing to the body-centered cubic (bcc),
hexagonal
close-packed (hcp), and face-centered cubic
(fcc)
structures. We observe
faceted equilibrium shapes and diffusion-controlled layerwise
crystal growth consistent with two- dimensional nucleation. The
predicted
growth anisotropies are discussed in relation with results from
experiment and
atomistic simulations. We also demonstrate that varying the lattice
constant of
a simple cubic substrate, one can tune the epitaxially growing body-centered tetragonal
structure
between bcc and fcc, and observe a Mullins-Sekerka/Asaro-Tiller-Grinfeld-type instability. [Phys.
Rev. Lett. 103, 035702 (2009)]
Classical
density functional theory methods in soft and hard matter
M. Haataja,1
L.
Gránásy,2,3 and H. Löwen4
1Department of Mechanical and Aerospace Engineering,
Institute for
the Science and Technology of Materials (PRISM) and Program in Applied
and
Computational Mathematics (PACM), Princeton University,Princeton
NJ 08544, USA
2Research Institute for Solid State Physics and Optics,
H-1525
Budapest, Hungary
3BCAST, Brunel University,
Uxbridge UB8
3PH, UK
4Department of Theoretical Physics, Heinrich-Heine-Universität
Düsseldorf, D-40225 Düsseldorf, Germany
Herein
we provide a brief summary of the background, events and
results/outcome of the
CECAM workshop ‘Classical density functional theory methods in soft and
hard
matter’ held in Lausanne between October 21 and October 23 2009, which
brought
together two largely separately working communities, both of whom
employ
classical density functional techniques: the soft-matter community and
the
theoretical materials science community with interests in phase
transformations
and evolving microstructures in engineering materials. After outlining
the
motivation for the workshop, we first provide a brief overview of the
articles
submitted by the invited speakers for this special issue of Journal
of
Physics: Condensed Matter, followed by a collection of outstanding
problems
identified and discussed during the workshop. [ J. Phys.: Condens.
Matter 22, 360301 (2010)]
 Polymorphism,
crystal nucleation and growth in the phase-field crystal model in 2d
and 3d
Polymorphism,
crystal nucleation and growth in the phase-field crystal model in 2d
and 3d
G. I. Tóth,1 G. Tegze,1
T.
Pusztai,1 G. Tóth,2 and
L. Gránásy1,3
1Research Institute for Solid State Physics and Optics,
H-1525
Budapest, Hungary
2Institute of Chemistry, Eötvös University, PO Box 32, H-1518 Budapest,
Hungary
3Brunel Centre for Advanced Solidification
Technology, Brunel University, Uxbridge
UB8 3PH, UK
We
apply a simple dynamical density functional theory, the phase-field
crystal
(PFC) model of overdamped conservative
dynamics, to
address polymorphism, crystal nucleation, and crystal growth in the
diffusion-controlled limit. We refine the phase diagram for 3D, and
determine
the line free energy in 2D and the height of the nucleation barrier in
2D and
3D for homogeneous and heterogeneous nucleation by solving the
respective
Euler–Lagrange (EL) equations. We demonstrate that, in the PFC model,
the
body-centered cubic (bcc), the face-centered cubic (fcc),
and the hexagonal close-packed structures (hcp)
compete, while the simple cubic structure is unstable, and that phase
preference can be tuned by changing the model parameters: close to the
critical
point the bcc structure is stable, while far from the critical point
the fcc prevails, with an hcp
stability domain in between. We note that with increasing distance from
the
critical point the equilibrium shapes vary from the sphere to specific
faceted
shapes: rhombic dodecahedron (bcc), truncated octahedron (fcc), and hexagonal
prism (hcp).
Solving the equation of motion of the PFC model supplied with conserved
noise,
solidification starts with the nucleation of an amorphous precursor
phase, into
which the stable crystalline phase nucleates. The growth rate is found
to be
time dependent and anisotropic; this anisotropy depends on the driving
force.
We show that due to the diffusion-controlled growth mechanism, which is
especially relevant for crystal aggregation in colloidal systems, dendritic growth structures evolve in
large-scale
isothermal single-component PFC simulations. An oscillatory effective
pair
potential resembling those for model glass formers has been evaluated
from
structural data of the amorphous phase obtained by instantaneous
quenching.
Finally, we present results for eutectic solidification in a binary PFC
model. [ J. Phys.: Condens.
Matter 22,
364101 (2010).]
 Phase-field
crystal modelling of crystal nucleation, heteroepitaxy and patterning
Phase-field
crystal modelling of crystal nucleation, heteroepitaxy and patterning
L.
Gránásy,1,2 G. Tegze,1
G. I.
Tóth,1 and T. Pusztai1
1Research Institute for Solid State Physics and Optics,
H-1525
Budapest, Hungary
2Brunel Centre for Advanced Solidification Technology, Brunel University, Uxbridge UB8 3PH, UK
A
simple dynamical density functional theory, the phase-field crystal
(PFC)
model, was used to describe homogeneous and heterogeneous crystal
nucleation in
two-dimensional (2D) monodisperse
colloidal systems
and crystal nucleation in highly compressed Fe liquid. External
periodic
potentials were used to approximate inert crystalline substrates in
addressing
heterogeneous nucleation. In agreement with experiments in 2D colloids,
the PFC
model predicts that in 2D supersaturated liquids, crystalline freezing
starts
with homogeneous crystal nucleation without the occurrence of the hexatic phase. At extreme supersaturations,
crystal nucleation happens after the appearance of an amorphous
precursor both
in two and three dimensions. Contrary to expectations based on the
classical
nucleation theory, it is shown that corners are not necessarily favourable places for crystal nucleation.
Finally, it is
shown that by adding external potential terms to the free energy, the
PFC
theory can be used to model colloid patterning experiments. [ Philos. Mag. 91, 123-149 (2011).]
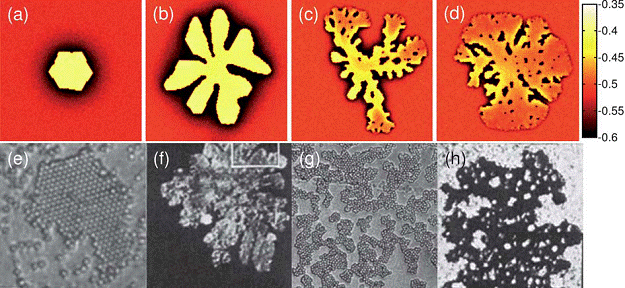 Tuning the structure
of non-equilibrium soft materials by varying the thermodynamic driving
force
for crystal ordering
Tuning the structure
of non-equilibrium soft materials by varying the thermodynamic driving
force
for crystal ordering
G.
Tegze,1 L. Gránásy,1,2
G. I.
Tóth,1 J. F. Douglas,3 and T. Pusztai1
1Research Institute for Solid State Physics and Optics,
H-1525
Budapest, Hungary
2Brunel Centre for Advanced Solidification Technology, Brunel University, Uxbridge UB8 3PH, UK
3Polymers Division, National Institute of
Standards and
Technology,Gaithersburg,
MD,
20899, USA.
The
present work explores the ubiquitous morphological changes in
crystallizing
systems with increasing thermodynamic driving force based on a novel
dynamic
density functional theory. A colloidal ‘soft’ material is chosen as a
model
system for our investigation since there are careful colloidal
crystallization
observations at a particle scale resolution for comparison, which
allows for a
direct verification of our simulation predictions. We particularly
focus on a
theoretically unanticipated, and generic, morphological transition
leading to
progressively irregular-shaped single crystals in both colloidal and
polymeric
materials with an increasing thermodynamic driving force. Our
simulation method
significantly extends previous ‘phase field’ simulations by
incorporating a
minimal description of the ‘atomic’ structure of the material, while
allowing
simultaneously for a description of large scale crystal growth. We
discover a
‘fast’ mode of crystal growth at high driving force, suggested before
in
experimental colloidal crystallization studies, and find that the
coupling of
this crystal mode to the well-understood ‘diffusive’ or ‘slow’ crystal
growth
mode (giving rise to symmetric crystal growth mode and dendritic
crystallization as in snowflakes by the Mullins–Sekerka
instability) can greatly affect the crystal morphology at high
thermodynamic
driving force. In particular, an understanding of this interplay
between these
fast and slow crystal growth modes allows us to describe basic
crystallization
morphologies seen in both colloidal suspensions with increasing
particle concentration
and crystallizing polymer films with decreasing temperature: compact
symmetric
crystals, dendritic crystals, fractal-like
structures, and then a return to compact symmetric single crystal
growth again.
[ Soft Matter 7, 1789-1799
(2011).]
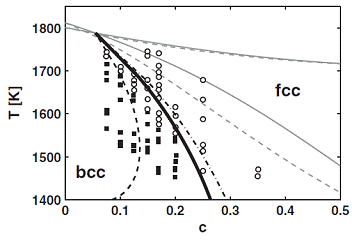 Ginzburg-Landau-type multiphase field model
for competing fcc
and bcc nucleation
Ginzburg-Landau-type multiphase field model
for competing fcc
and bcc nucleation
G.
I. Tóth,1 J. R. Morris,2
and L.
Gránásy1,3
1Research Institute for Solid State Physics and Optics,
H-1525 Budapest,
Hungary
2Oak Ridge National Laboratory, Oak Ridge,
Tennessee
37830, USA
3BCAST, Brunel University,
Uxbridge,
Middlesex, UB8 3PH, United Kingdom
We
address crystal nucleation and fcc-bcc
phase
selection in alloys using a multiphase field model that relies on Ginzburg-Landau free energies of the liquid-fcc, liquid-bcc, and fcc-bcc
subsystems, and determine the properties of the nuclei as a function of
composition, temperature, and structure. With a realistic choice for
the free
energy of the fcc-bcc interface, the model
predicts
well the fcc-bcc phase-selection boundary
in the
Fe-Ni system. [ Phys. Rev. Lett.
105, 045701 (2011).]
 Faceting and branching in 2D crystal growth
Faceting and branching in 2D crystal growth
G.
Tegze,1 G. I. Tóth,1
and L.
Gránásy1,2
1Research Institute for Solid State Physics and Optics,
H-1525
Budapest, Hungary
2BCAST, Brunel
University,
Uxbridge, Middlesex, UB8 3PH, United Kingdom
Using atomic scale
time-dependent
density functional calculations we confirm that both
diffusion-controlled and diffusionless
crystallization modes exist in simple 2D
systems. We provide theoretical evidence that a faceted to nonfaceted
transition is coupled to these crystallization modes, and faceting is
governed
by the local supersaturation at the
fluid-crystalline
interface. We also show that competing modes of crystallization have a
major
influence on mesopattern formation.
Irregularly
branched and porous structures are emerging at the crossover of the
crystallization modes. The proposed branching mechanism differs
essentially
from dendritic fingering driven by
diffusive
instability.
Video #1
Video #2
[ Phys. Rev. Lett.
106, 195502 (2011).]
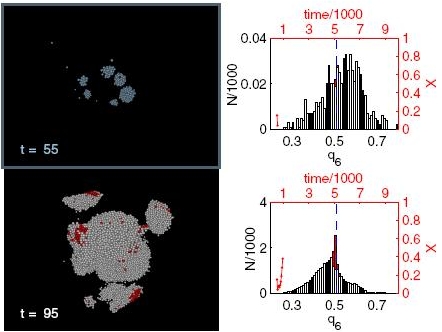 Amorphous
nucleation precursor in highly nonequilibrium fluids
Amorphous
nucleation precursor in highly nonequilibrium fluids
G.
I. Tóth,1 T. Pusztai,1 G. Tegze,1 G. Tóth,2 and L.
Gránásy1,3
1Research Institute for Solid State Physics and Optics, P.O. Box 49 ,H-1525
Budapest, Hungary
2Institute of Chemistry, Eötvös University,
P.O. Box 32, H-1518, Budapest, Hungary
3BCAST, Brunel University,
Uxbridge,
Middlesex, UB8 3PH, United Kingdom
Dynamical density-functional simulations
reveal structural aspects of crystal nucleation in undercooled liquids:
The first appearing solid is amorphous, which promotes the nucleation
of bcc crystals but suppresses the appearance of the fcc and hcp
phases. These findings are associated with features of the effective
interaction potential deduced from the amorphous structure. [ Phys. Rev. Lett.
107, 1 75702 (2011).]
 Selected
issues of phase-field crystal simulations
Selected
issues of phase-field crystal simulations
H. Emmerich1, L.
Gránásy2,3
2Research
Institute for Solid State Physics and Optics, H-1525
Budapest, Hungary
1Institut
für Theoretische Physik II: Weiche Materie, Heinrich-Heine-Universitát
Düsseldorf, Germany
In
this contribution our focus is on the phase-field crystal method, which
can be viewed as the youngest methodology in the field of interface
computation based on recent work by Elder et al. (Phys. Rev. Lett. 88,
245701 (2002)). It bridges the gap between the molecular simulation
approaches and the phase-field approach by operating on diffusive time
scales yet atomic length scales. Here we review the fundaments of the
phase-field crystal method as well as different models established so
far with the aim to capture the main features of the wide range of
phase diagrams found in
materials science more and more comprehensively. [ Eur.
Phys. J. Plus
126, 102 (2011).]
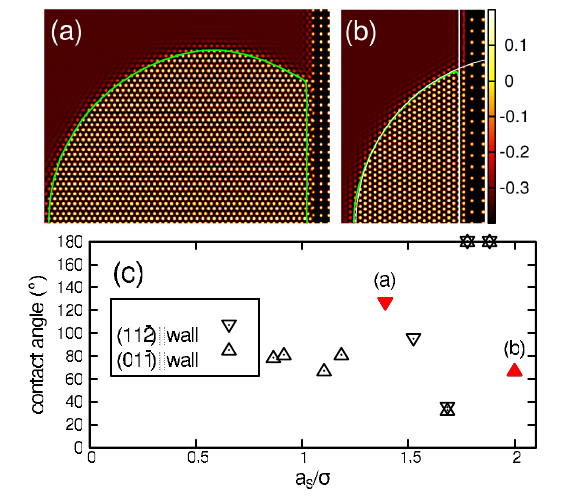 Heterogeneous Crystal Nucleation: The Effect of Lattice Mismatch
Heterogeneous Crystal Nucleation: The Effect of Lattice Mismatch
Gyula I. Toth1, György Tegze 1, Tamás Pusztai 1, and László Gránásy1,2
1Research Institute for Solid State Physics and Optics, P.O. Box 49, H-1525
Budapest, Hungary
2BCAST, Brunel University,
Uxbridge,
Middlesex, UB8 3PH, United Kingdom
A simple dynamical density functional theory is used to investigate freezing of an undercooled liquid in
the presence of a crystalline substrate. We find that the adsorption of the crystalline phase on the substrate,
the contact angle, and the height of the nucleation barrier are nonmonotonic functions of the lattice
constant of the substrate. We show that the free-growth-limited model of particle-induced freezing by
Greer et al. [Acta Mater. 48, 2823 (2000)] is valid for larger nanoparticles and a small anisotropy of the
interface free energy. Faceting due to the small size of the foreign particle or a high anisotropy decouples
free growth from the critical size of homogeneous nuclei.
[ Phys. Rev. Lett.
108, 025502 (2012).]
 Phase-field-crystal models for condensed matter dynamics on atomic length
and diffusive time scales: an overview
Phase-field-crystal models for condensed matter dynamics on atomic length
and diffusive time scales: an overview
Heike Emmerich1, Hartmut Löwen2, Raphael Wittkowski2, Thomas Gruhn1, Gyula I. Tóth3, György Tegze3 and László Gránásy3,4
1Lehrstuhl für Material- und Prozesssimulation, Universität Bayreuth, D-95440 Bayreuth, Germany
2Institut für Theoretische Physik II, Weiche Materie, Heinrich-Heine-Universität Düsseldorf, D-40225 Düsseldorf, Germany
3Institute for Solid State Physics and Optics, Wigner Research Centre for Physics,
PO Box 49, H-1525 Budapest, Hungary
4BCAST, Brunel University, Uxbridge, Middlesex UB8 3PH, UK
Here, we review the basic concepts and applications of the phase-field-crystal (PFC) method, which is one of the latest simulation methodologies in materials science for problems, where atomic- and microscales are tightly coupled. The PFC method operates on atomic length and diffusive time scales, and thus constitutes a computationally efficient alternative to molecular simulation methods. Its intense development in materials science started fairly recently fol- lowing the work by Elder et al. [Phys. Rev. Lett. 88 (2002), p. 245701]. Since these initial studies, dynamical density functional theory and thermodynamic concepts have been linked to the PFC approach to serve as further theoretical fundamentals for the latter. In this review, we summarize these methodological development steps as well as the most important applications of the PFC method with a special focus on the interaction of development steps taken in hard and soft matter physics, respectively. Doing so, we hope to present today's state of the art in PFC modelling as well as the potential, which might still arise from this method in physics and materials science in the nearby future. [Advances in Physics, 61, 665-743 (2012)]
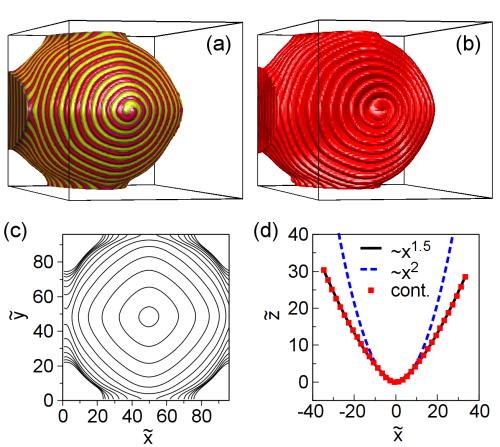 Spiraling eutectic dendrites
Spiraling eutectic dendrites
Tamás Pusztai1, László Rátkai1, Attila Szállás1 and László Gránásy1,2
1 Institute for Solid State Physics and Optics, Wigner Research Centre for Physics, P.O. Box 49, Budapest H-1525, Hungary
2BCAST, Brunel University, Uxbridge, Middlesex, UB8 3PH, United Kingdom
Eutectic dendrites forming in a model ternary system have been studied using the phase-field theory. The eutectic and one-phase dendrites have similar forms, and the tip radius scales with the interface free energy as for one-phase dendrites. The steady-state eutectic patterns, appearing on these two-phase dendrites, include concentric rings and single- to multiarm spirals from which the fluctuations choose; a stochastic phenomenon characterized by a peaked probability distribution. The number of spiral arms correlates with the tip radius and the kinetic anisotropy. [Phys. Rev. E, 87, 032401 (2013)]
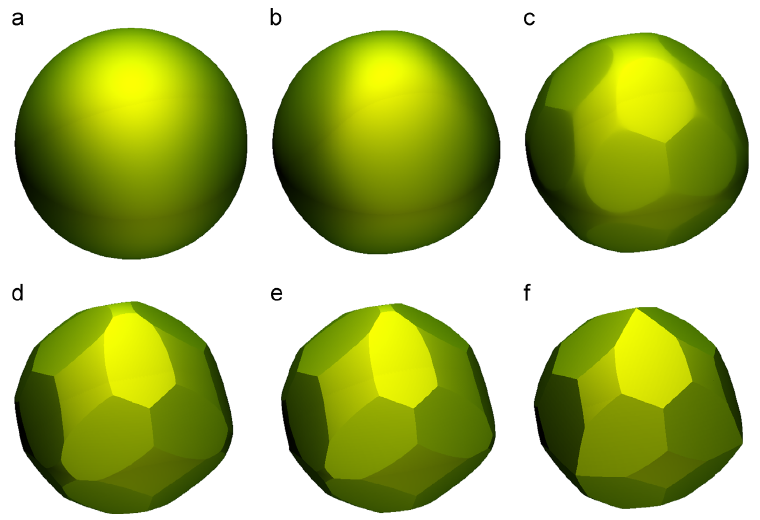 Free energy of the bcc-liquid interface and the Wulff shape as predicted by the phase-field crystal model
Free energy of the bcc-liquid interface and the Wulff shape as predicted by the phase-field crystal model
Frigyes Podmaniczky1, Gyula I. Tóth1, Tamás Pusztai1, László Gránásy1,2
1 Institute for Solid State Physics and Optics, Wigner Research Centre for Physics, P.O. Box 49, Budapest H-1525, Hungary
2BCAST, Brunel University, Uxbridge, Middlesex, UB8 3PH, United Kingdom
The Euler-Lagrange equation of the phase-field crystal (PFC) model has been solved under appropriate boundary conditions to obtain the equilibrium free energy of the body centered cubic crystal-liquid interface for 18 orientations at various reduced temperatures in the range ε∈[0,0.5]. While the maximum free energy corresponds to the {100} orientation for all ε values, the minimum is realized by the {111} direction for smaller ε(<0.13), and by the {211} orientation for higher ε. The predicted dependence on the reduced temperature is consistent with the respective mean field critical exponent. The results are fitted with an eight-term Kubic harmonic series, and are used to create stereographic plots displaying the anisotropy of the interface free energy. We have also derived the corresponding Wulff shapes that vary with increasing ε from sphere to a polyhedral form that differs from the rhombo-dodecahedron obtained previously by growing a bcc seed until reaching equilibrium with the remaining liquid. [Journal of Crystal Growth, 385, 148-153 (2014)]
 Phase-Field Modeling of Polycrystalline Solidification: From Needle Crystals to Spherulites - A Review
Phase-Field Modeling of Polycrystalline Solidification: From Needle Crystals to Spherulites - A Review
László Gránásy1,2, László Rátkai1, Attila Szállás1, Bálint Korbuly1, Gyula I. Tóth1, László Környei3, Tamás Pusztai1
1 Institute for Solid State Physics and Optics, Wigner Research Centre for Physics, P.O. Box 49, Budapest H-1525, Hungary
2BCAST, Brunel University, Uxbridge, Middlesex, UB8 3PH, United Kingdom
3Department of Mathematics and Computational Sciences, Széchenyi István University, Győr 9026, Hungary
Advances in the orientation-field-based phase-field (PF) models made in the past are reviewed. The models applied incorporate homogeneous and heterogeneous nucleation of growth centers and several mechanisms to form new grains at the perimeter of growing crystals, a phenomenon termed growth front nucleation. Examples for PF modeling of such complex polycrystalline structures are shown as impinging symmetric dendrites, polycrystalline growth forms (ranging from disordered dendrites to spherulitic patterns), and various eutectic structures, including spiraling two-phase dendrites. Simulations exploring possible control of solidification patterns in thin films via external fields, confined geometry, particle additives, scratching/piercing the films, etc. are also displayed. Advantages, problems, and possible solutions associated with quantitative PF simulations are discussed briefly. [Metall. Mater. Trans. A, 45, 1694-1719 (2013)]
 Nonlinear hydrodynamic theory of crystallization
Nonlinear hydrodynamic theory of crystallization
Gyula I. Tóth1, László Gránásy1,2, György Tegze1
1Institute for Solid State Physics and Optics, Wigner Research Centre for Physics, P.O. Box 49, Budapest H-1525, Hungary
2BCAST, Brunel University, Uxbridge, Middlesex, UB8 3PH, United Kingdom
We present an isothermal fluctuating nonlinear hydrodynamic theory of crystallization in molecular liquids. A dynamic coarse-graining technique is used to derive the velocity field, a phenomenology which allows a direct coupling between the free energy functional of the classical density functional theory and the Navier-Stokes equation. In contrast to the Ginzburg-Landau type amplitude theories, the dynamic response to elastic deformations is described by parameter-free kinetic equations. Employing our approach to the free energy functional of the phase-field crystal model, we recover the classical spectrum for the phonons and the steady-state growth fronts. The capillary wave spectrum of the equilibrium crystal-liquid interface is in good qualitative agreement with the molecular dynamics simulations. [J. Phys.: Condens. Matter 26, 055001 (2014)]
 Crystallization: Colloidal suspense
Crystallization: Colloidal suspense
László Gránásy1,2, Gyula I. Tóth1,
1Institute for Solid State Physics and Optics, Wigner Research Centre for Physics, P.O. Box 49, Budapest H-1525, Hungary
2BCAST, Brunel University, Uxbridge, Middlesex, UB8 3PH, United Kingdom
According to classical nucleation theory, a crystal grows from a small nucleus that already bears the symmetry of its end phase - but experiments with colloids now reveal that, from an amorphous precursor, crystallites with different structures can develop. [Nature Physics - News and Views, 10, pages 12-13 (2014)]
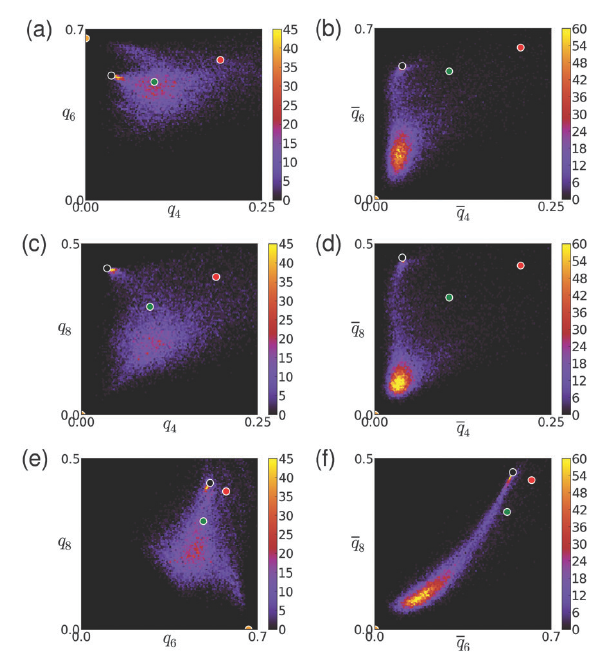 Heterogeneous nucleation of/on nanoparticles: a density functional study using the phase-field crystal model
Heterogeneous nucleation of/on nanoparticles: a density functional study using the phase-field crystal model
L. Gránásy1,2, F. Podmaniczky1, G.I. Tóth1, G. Tegze1, T. Pusztai1
1Institute for Solid State Physics and Optics, Wigner Research Centre for Physics, P.O. Box 49, Budapest H-1525, Hungary
2BCAST, Brunel University, Uxbridge, Middlesex, UB8 3PH, United Kingdom
Crystallization of supersaturated liquids usually starts by heterogeneous nucleation. Mounting evidence shows that even homogeneous nucleation in simple liquids takes place in two steps; first a dense amorphous precursor forms, and the crystalline phase appears via heterogeneous nucleation in/on the precursor cluster. Herein, we review recent results by a simple dynamical density functional theory, the phase-field crystal model, for (precursor-mediated) homogeneous and heterogeneous nucleation of nanocrystals. It will be shown that the mismatch between the lattice constants of the nucleating crystal and the substrate plays a decisive role in determining the contact angle and nucleation barrier, which were found to be non-monotonic functions of the lattice mismatch. Time dependent studies are essential as investigations based on equilibrium properties often cannot identify the preferred nucleation pathways. Modeling of these phenomena is essential for designing materials on the basis of controlled nucleation and/or nano-patterning. [Chem. Soc. Rev. 43, 2159-2173 (2014)]
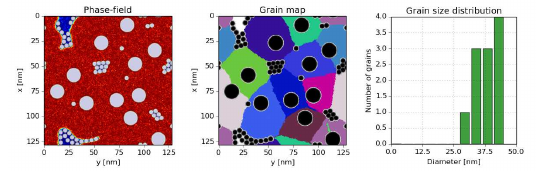 Phase-Field Modeling of Solidification in Light-Metal Matrix Nanocomposites
Phase-Field Modeling of Solidification in Light-Metal Matrix Nanocomposites
T. Pusztai1, L. Rátkai1, A. Szállás1, L. Gránásy1,2
1Institute for Solid State Physics and Optics, Wigner Research Centre for Physics, P.O. Box 49, Budapest H-1525, Hungary
2BCAST, Brunel University, Uxbridge, Middlesex, UB8 3PH, United Kingdom
The quantitative phase-field approach has been adapted to model solidification in the presence of Metal Matrix Nanocomposites (MMNCs) in a single-component liquid. Nanoparticles of fixedsize and shape are represented by additional fields. The corresponding equations of motion are assumed to ensure relaxation dynamics, and can be supplemented by random forces (realizing Brownian motion) or external fields. The nanoparticles are characterized by two model parameters: their mobility and the contact angle they realize with the solid-liquid interface. We investigate the question how grain size distribution can be influenced by heterogeneous nucleation on the nanoparticles and by the front-particle interaction. We explore, furthermore, how materials and process parameters, such as temperature, density and size/shape distribution of the nanoparticles, influence microstructure evolution.. [In "Magnesium Technology 2014", eds. M. Alderman, M.V. Manuel, N. Hort, N.R. Neelameggham (The Minerals, Metals and Materials Sociesty/Wiley, Hoboken, 2014), pp. 455-460. ISBN: 978-1-118-88816-2]