RMC

  RMC++ examples

This page shows some examples of early RMC++ studies.

These simulations were made by the original RMC++ code, but the conclusions are valid for the later versions as well.

  Liquid CCl4

Liquid CCl4 provides a nice example of the use of RMC++:



The data

The data used were obtained by neutron diffraction at the Budapest PSD neutron diffractometer.
The data Q-range is 0.55 to 9.15 ů¹, in 100 points (irregularly sampled).

Configuration size

The density of our sample is 0.0319 atoms per cubic Å. A configuration with 1000 atoms (200 molecules) would fit in a cubic box of dimension 31.53 Å (which is adequate if there is no long range order beyond 31.53 / 2=15.76 Å).
However, for the sake of statistical accuracy, a greater number of molecules is necessary, and we choose to build a configuration with 2048 molecules, i.e. 10240 atoms.
This yields a cubic box of size 68.4704 Å, i.e. a histogram range of 34.23522 Å (in the standard version, i.e. without the RMC++ extension).
This size complies with the requirement imposed by the Q-range of the data: the greatest distance binned in the histograms must be at least 2 π / 0.55= 11.4 Å (one full r-period for the lowest Q value).

(n.b. the reason for using 4 or 5 decimals accuracy does obviously not derive from physics, but from numerical requirements)

Histograms bin width

The highest Q value imposes that the bin width dr is at most 2 π / (5 x 9.15)= 0.137 Å.

With a configuration of 2048 molecules, one can attempt a bin width of 0.1 Å. The validity of this choice can be checked a posteriori by looking at the histograms.
If there are not enough distances to secure the information on wants to derive from the run, then the size of the configuration or the size of the histogram bins can be increased.

Distances of closest approach (cutoffs)

The distances of closest approach between atoms are defined from external a priori information: previous runs, other experiments, known structure, guesses... In the worst case it can be imposed by the density. But in practice, they have to be adjusted due to the necessity to allow individual atoms to move.
(n.b.: if the cutoffs have to be made smaller than a value known to be true in order to allow the configuration to evolve, then the resulting configuration is not realistic)

In the CCl4 case, we chose the cutoffs as follows:

These were partly imposed by the molecular geometry, although with RMC++, individual molecules are defined by the fixed neighbours constraints (FNC), which overrides the cutoffs (i.e. within one molecule, the cutoffs can be not satisfied if this is imposed by the FNC).

Fixed neighbours constraints

We take advantage of the FNC to mimic the individual CCl4 molecules, i.e. we define links and allowed distance ranges between given atoms so that the geometry of the CCl4 molecules is reproduced.
The FNC's are defined by the molecule geometry. For CCl4 there are just two constraints:

In defining these distances, it is important to keep in mind that the configuration evolves by moving atoms individually. Therefore, the constraints must leave a certain freedom of movement to the atoms, in order to allow the configuration to evolve. If the geometry of the molecule imposes very strict FNC's (e.g. flat or rigid molecules) then the individual moves of atoms is ruled out if one wants to obtain a realistic configuration. In this case, the molecules have to be moved as a whole, this is possible with RMCmol (under development).

Move amplitudes

The amplitude of the individual atomic moves is defined in the .dat file of run parameters. It has to be adjusted to allow the configuration to evolve. Small moves will be more likely to be accepted, but with a small effect, yielding a slow evolution. On the contrary, large moves will make big steps, but with a larger probability of being rejected (see the discussion in the RMCA manual).
Therefore, in practice, these amplitudes are often adjusted after a few test runs.
Note that the move amplitudes are defined by the maximum range in each direction (and therefore the effective range is greater by a factor 1.732).
For CCl4, we used maximum moves of 0.1 Å.

Making the starting configuration

There are programmes to create starting configurations (see the download page).
If there is enough space for molecules to move, a simple recipe is to

At this stage, one should have a `good starting configuration'.

The RMC run

From a `good starting configuration', the run parameters can be fine-tuned. Experience shows that the RMC result does not depend on the starting configuration.
The duration of the run is very variable, depending on the problem.
For CCl4, starting from a good configuration, we made a 20 hours run (on a 2 Pentium III processor 500 Mhz PC).
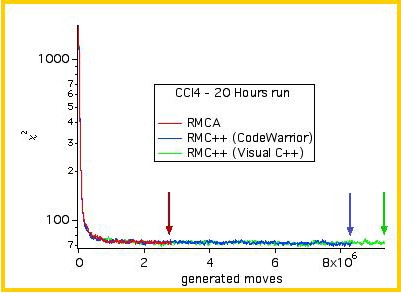
The convergence of the algorithm is shown below, for the three different codes: RMCA (fortran) and RMC++ (2 different compilers).

The evolution of the χ² is typical of a RMC run.
Incidentally, the figure above shows that RMC++ is 2~3 times as fast as RMCA.


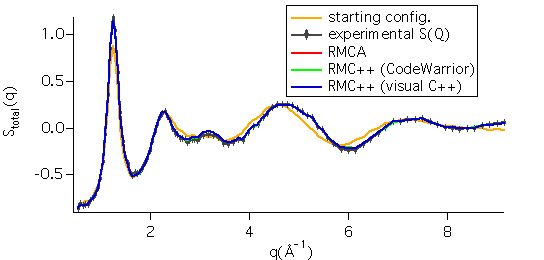
The results

The run results consist in the configuration, and the partials in the .out file, which allow direct visualisation of the fit to the data:

It can be seen that the starting configuration was rather good, and that the RMC fits are excellent.

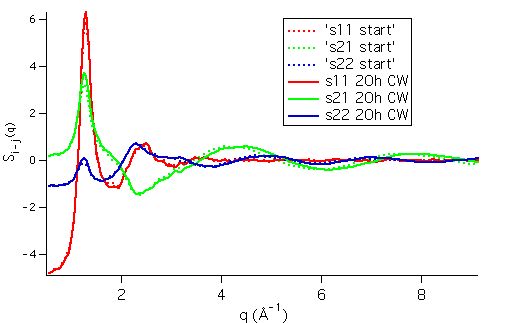
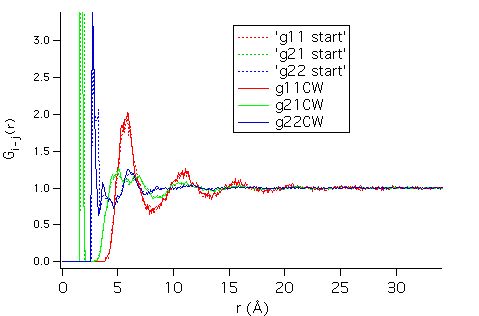
Individual partial structure factors appear below:

and the partial pair correlation functions are shown below:

The first intramolecular peaks C-Cl and Cl-Cl dominate the graph.
Long range order appears via the C-C partial (up to 20 ů¹), and is due to the arrangement of neighbouring molecules. As required by the calculation of the sine-Fourier transform, the g(r)'s are equal to 0 at the largest calculated distances.
This `local arrangement' gives the intermolecular contribution to the C-Cl and Cl-Cl partials.

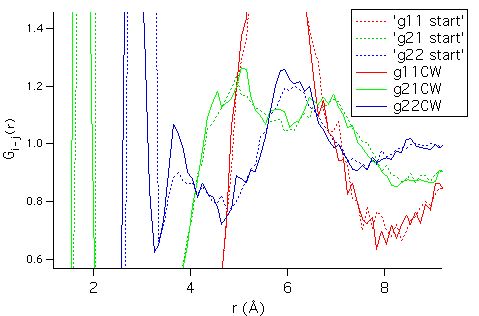
A detailed view of the g(r) partials appear below:

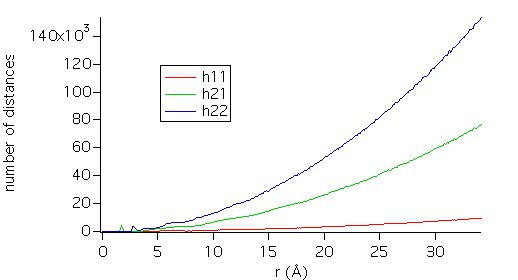
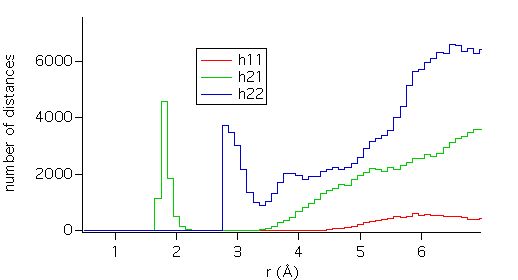
Note the statistical oscillations that appear on the detailed level. The significance, or an estimate of the uncertainty about the g(r) values derived from the RMC run can be guessed by looking directly at the histograms. They appear below:

The number of distances grows as r¯². But one is usually interested in the short range deviation from perfect homogeneity, which appears as small peaks, as seen in the detail below.

The configuration does much more than just allow to calculate the g(r) partials without the usual problems of direct sine-Fourier transformation. It is possible to calculate cosine distributions, etc...
Developing tools for exploiting RMC results actually appears as important as implementing the RMC algorithm itself.

 

 Run Reports


Here are some RMC run reports on a variety of materials (files in pdf format). The simulations were performed by the original RMC++ code by Guillaume Evrard.

The following runs were dedicated to the investigation of the effect of algorithmic constraints rather than the study of the materials themselves.

Top of page

Last modified 04/03/2023) by Orsolya Gereben
(comments welcome!)