Rheology of dense granular flows for elongated particles
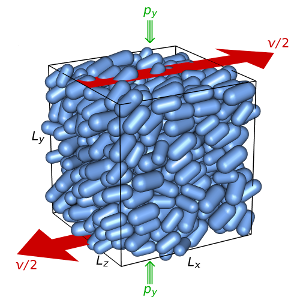
We study the rheology of dense granular flows for frictionless spherocylinders by 3D numerical simulations. As for spherical particles, the effective friction µ is an increasing function of the inertial number I, and we systematically investigate the dependence of µ on the particle aspect ratio Q, as well as that of the normal stress differences, the volume fraction and the coordination number. We show in particular that the quasi-static friction coefficient is nonmonotonic with Q: from the spherical case Q=1 , it first sharply increases, reaches a maximum around Q≃1.05 , and then gently decreases until Q=3, passing its initial value at Q≃2. We provide a microscopic interpretation for this unexpected behavior through the analysis of the distribution of dissipative contacts around the particles: as compared to spheres, slightly elongated grains enhance contacts in their central cylindrical band, whereas at larger aspect ratios particles tend to align and dissipate by preferential contacts at their hemispherical caps.Phys. Rev. E 96, 062903 (2017) • pdf
EPJ Web Conf. 140, 03062 (2017) • pdf
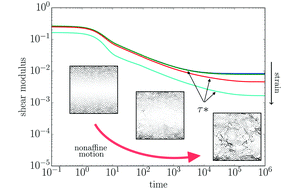
Softening and yielding of soft glassy materials
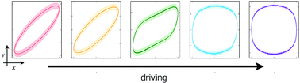
Solids deform and fluids flow, but soft glassy materials, such as emulsions, foams, suspensions, and pastes, exhibit an intricate mix of solid- and liquid-like behavior. While much progress has been made to understand their elastic (small strain) and flow (infinite strain) properties, such understanding is lacking for the softening and yielding phenomena that connect these asymptotic regimes. Here we present a comprehensive framework for softening and yielding of soft glassy materials, based on extensive numerical simulations of oscillatory rheological tests, and show that two distinct scenarios unfold depending on the material’s packing density. For dense systems, there is a single, pressure-independent strain where the elastic modulus drops and the particle motion becomes diffusive. In contrast, for weakly jammed systems, a two-step process arises: at an intermediate softening strain, the elastic and loss moduli both drop down and then reach a new plateau value, whereas the particle motion becomes diffusive at the distinctly larger yield strain. We show that softening is associated with an extensive number of microscopic contact changes leading to a non-analytic rheological signature. Moreover, the scaling of the softening strain with pressure suggest the existence of a novel pressure scale above which softening and yielding coincide, and we verify the existence of this crossover scale numerically. Our findings thus evidence the existence of two distinct classes of soft glassy materials - jamming dominated and dense - and show how these can be distinguished by their rheological fingerprint.Soft Matter 13, 9036-9045 (2017) • pdf
Stress relaxation in viscous soft spheres
We report the results of molecular dynamics simulations of stress relaxation tests in athermal viscous soft sphere packings close to their unjamming transition. By systematically and simultaneously varying both the amplitude of the applied strain step and the pressure of the initial condition, we access both linear and nonlinear response regimes and control the distance to jamming. Stress relaxation in viscoelastic solids is characterized by a relaxation time τ* that separates short time scales, where viscous loss is substantial, from long time scales, where elastic storage dominates and the response is essentially quasistatic. We identify two distinct plateaus in the strain dependence of the relaxation time, one each in the linear and nonlinear regimes. The height of both plateaus scales as an inverse power law with the distance to jamming. By probing the time evolution of particle velocities during relaxation, we further identify a correlation between mechanical relaxation in the bulk and the degree of non-affinity in the particle velocities on the micro scale.Soft Matter 13, 6870-6876 (2017) • pdf
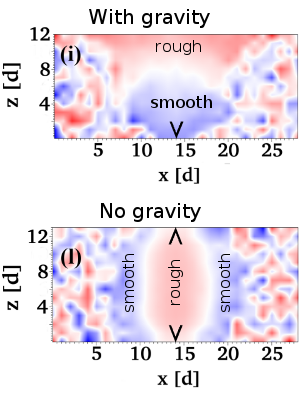
Shear-driven segregation of dry granular materials with different friction coefficients
It is well known that granular mixtures subjected to shear or vibration often segregate due to differences in particle size or density. We report the first experimental demonstration of bulk segregation in a shear-driven dry granular mixture, where the particles only differ in their surface friction coefficients. We found that the smoother particles tend to sink to the bottom of the shear zone, while rough particles migrate to the top of the sample. This phenomenon is similar to the well known kinetic sieving in particle mixtures with size heterogeneity. In the present case the smooth particles have a higher probability to penetrate into voids created by the shearing than the rough ones. We carried out discrete element simulations as well, and reproduced the experimentally observed segregation patterns. Moreover, simulations performed in the absence of gravity revealed, that rough particles tend to stay in the shear zone, while the smooth particles are being expelled from it. We propose a mechanism, in which the smooth particles are driven towards regions of lower shear rate.Soft Matter 13, 415-420 (2017)
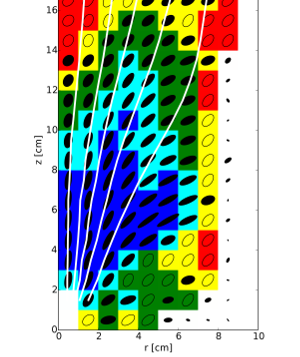
Packing, alignment and flow of shape-anisotropic grains in a 3D silo
Granular material flowing through bottlenecks like the openings of silos tend to clog and inhibit further flow. We study this phenomenon in a three-dimensional hopper for spherical and non-spherical particles by X-ray tomography. From the X-ray tomograms we determine the position and orientation of each particle in the bulk, as well as from subsequent tomogram pairs we can infer streamlines. We found that similarly to simple shear flows, the average orientation of the particles encloses a certain angle with the streamlines. Both this angle and the order parameter evolve as the grains travel downwards to silo, and the local shear deformation grows. Near the outlet the density distribution averaged over many clogged configurations provides information about the shape of a typical dome, which depends on the particle shape.New J. Phys. 18, 093017 (2016) • pdf
EPJ Web Conf. 140, 06017 (2017) • pdf
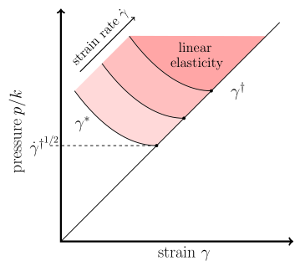
Beyond linear elasticity: Jammed solids at finite shear strain and rate
The shear response of soft solids can be modeled with linear elasticity, provided the forcing is slow and weak. However, both of these approximations break down when the material loses rigidity, such as in foams and emulsions at their jamming point. When deformations are applied too quickly, the material becomes stiffer. On the other hand, when deformations are too large, the material softens and eventually flows. Using computer simulations of athermal soft sphere packings we identified characteristic strain and time scales that quantify how and when the window of linear elasticity closes, and relate these scales to changes in the microscopic contact network. Our findings indicate that the mechanical response of jammed solids are generically nonlinear and rate-dependent on experimentally accessible strain and time scales.Soft Matter 12, 5450-5460 (2016) • pdf
Heaping, secondary flow and broken symmetry in flows of elongated granular particles
We shear granular rods in split-bottom geometry experiments, and find that a significant heap of height of at least 40% of the filling height can form at the particle surface. The heaping is caused by a significant secondary flow, which is absent for spherical particles. Flow reversal transiently reverses the secondary flow, leading to a quick collapse and slower regeneration of the heap. We present a symmetry argument and experimental data that show that the misalignment of the mean particle orientation with the streamlines is necessary for the secondary flow.Soft Matter 11, 2570-2576 (2015) • pdf
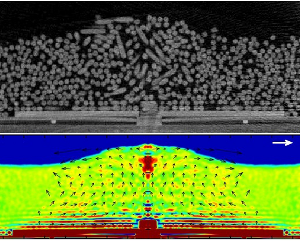
Evolution of granular shear zones
We investigated experimentally (surface imaging, bulk MRI and bulk x-ray CT) the evolution of wide shear zones. We compared granular materials consisting of spherical particles, irregular grains (like sand) and elongated particles. For initially random samples the shear zone width significantly decreases until shear strain of order unity (slightly larger strain for more anisotropic particles). Afterwards the shear zone width increases sligtly, especially for elongated particles. The evolution of the zone width is connected to both the shear induced density change, and (for nonspherical particles) the shear induced alignment of the particles. The final zone width is significantly smaller for irregular grains than for spherical particles. We modeled numerically the system with a suitably adjusted fluctuating band model.Phys. Rev. E 90, 032205 (2014) • pdf
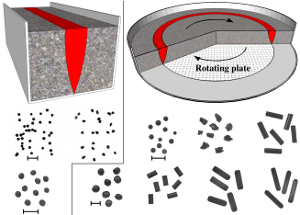
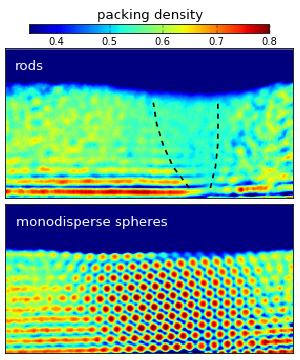
How does the particle shape affect the density of sheared granular materials?
Granular materials exposed to shear show a variety of unique phenomena: Reynolds dilatancy, positional order and orientational order are all present in the shear zone. In this experimental work we used x-ray tomography to investigate granulates consisting of macroscopic prolate (wooden dowel pins), oblate (chocolate lentils) and spherical grains (peas and airsoft gun ammunitions) in a cylindrical split bottom shear cell. We found that for non-spherical particles two opposite effects compete in the shear zone: the sheared granulate Reynolds dilates, and the particles become aligned which enable more compact structures. The complex rearrangements lead to a depression of the surface above the well oriented region of the shear zone, while neigbouring parts still show the effect of dilation in the form of heaps. For spherical grains the surface remains rather flat. Monodisperse spheres crystallize in the shear zone, their pair distribution function shows long range order. However, already slight deviations from the ideal monodisperse sphere shape inhibit crystallization.Soft Matter 10, 5157-5167 (2014) • pdf