 |
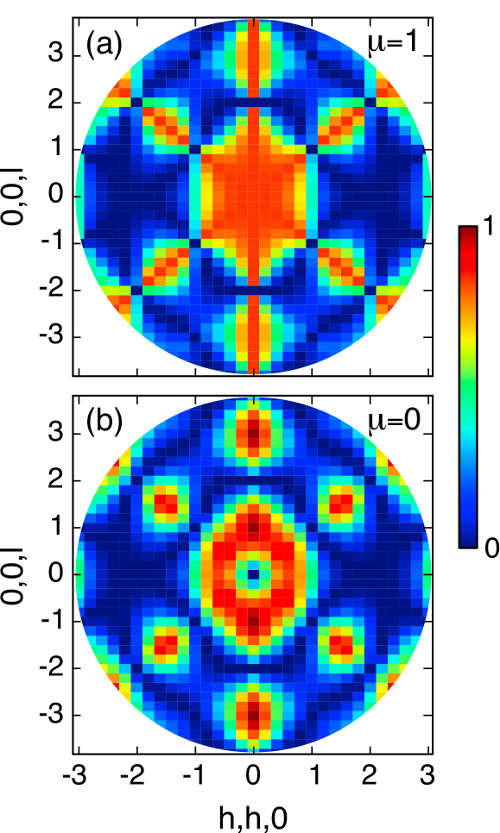
Quantum Ice
Water ice comprises a loosely-packed lattice of water molecules, held together by hydrogen bonds. This structure hides a puzzle — chemical bonding alone does not select a unique orientation of the water molecules. As a result each water molecule has a finite ground state entropy s0 ≈ kB log(3/2), in violation of the third law of thermodynamics. The same degeneracy, and the same contradiction, arises in problems of frustrated charge order on the pyrochlore lattice, and in the family of rare-earth magnets collectively known as spin ice. Of particular interest at the moment are "quantum spin ice" materials, where large quantum fluctuations may permit tunnelling between different ice states. Here we show how such tunnelling can lift the degeneracy of a spin or charge ice, stabilising a unique "quantum ice" ground state. This quantum ice has excitations described by the Maxwell action of 3+1 – dimensional quantum electrodynamics. We further show how such a quantum ice state might be distinguished in neutron scattering experiments on a spin ice material.
Nic Shannon, Olga Sikora, Frank Pollmann, Karlo Penc, Peter Fulde, Phys. Rev. Lett. 108, 067204/1-5 (2012)
|
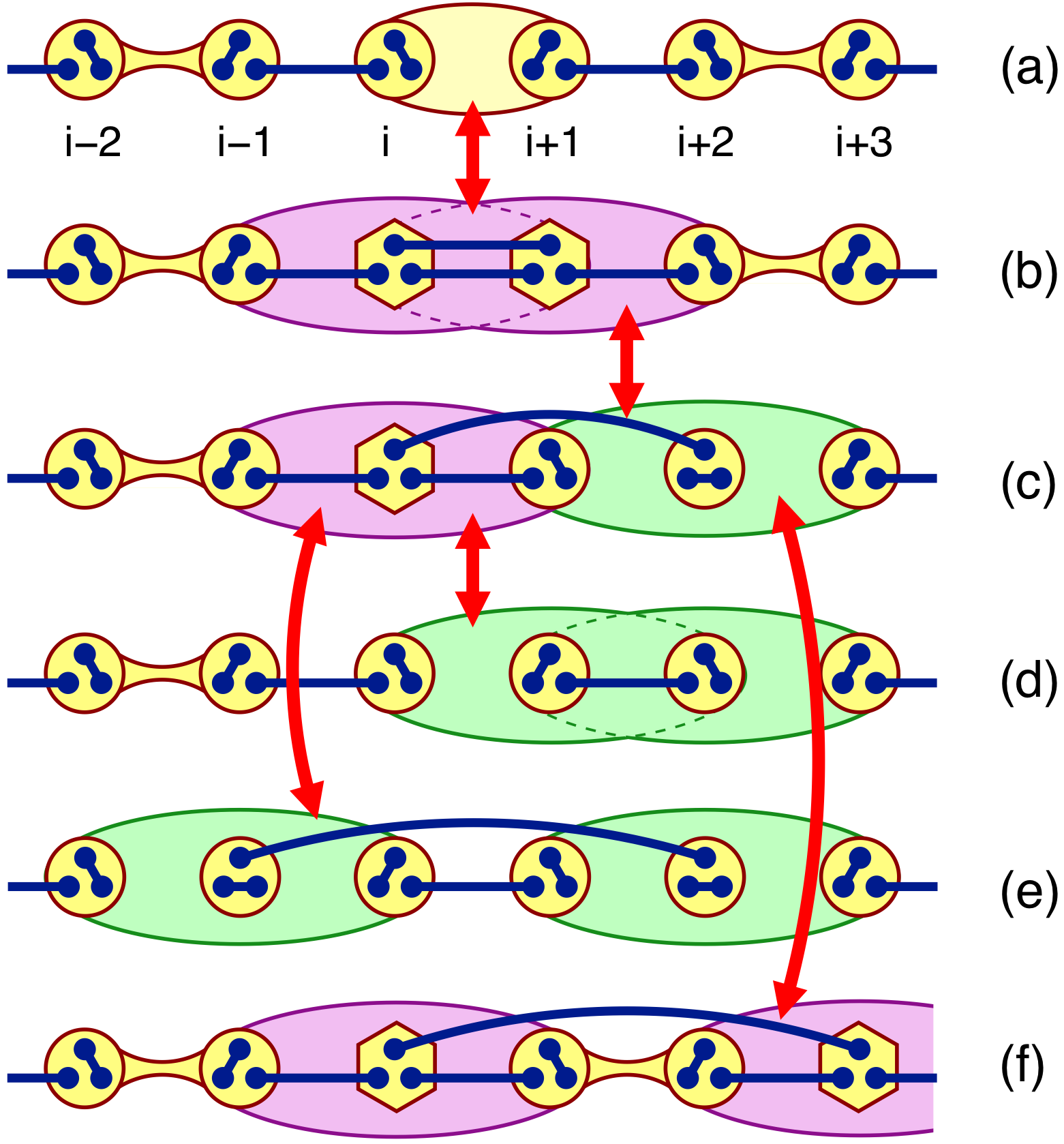 |
Exact ground states with deconfined gapless excitations for the 3 leg spin-1/2 tube
We consider a 3-leg spin-1/2 ladder with periodic boundary conditions (a spin tube) with a Hamiltonian given by two projection operators, one on the triangles, and the other on the square plaquettes on the side of the tube, that can be written in terms of Heisenberg and four spin ring exchange interactions. Depending on the relative strength of these two operators, we identify 3 phases: (i) for strongly antiferromagnetic exchange on the triangles, an exact dimerized ground state wave function with a gapped spectrum can be given as an alternation of spin and chirality valence bonds between nearest triangles; (ii) for ferromagnetic exchanges on the triangle we recover the phase of the spin-3/2 Heisenberg chain; (iii) between these two phases a gapless incommensurate phase exists. Furthermore, we explicitly construct an exact ground state wave function with two deconfined domain walls and gapless excitation spectrum at the quantum phase transition point between the incommensurate and dimerized phase.
Miklós Lajkó, Philippe Sindzingre, Karlo Penc, arXiv:1107.5501
|
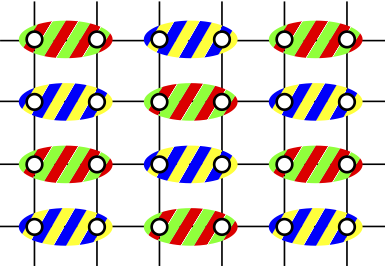 |
Simultaneous dimerization and SU(4) symmetry breaking of 4-color fermions on the square lattice
Using infinite project entangled pair states (iPEPS), exact diagonalization, and flavor-wave theory, we show that the SU(4) Heisenberg model undergoes a spontaneous dimerization on the square lattice, in contrast to its SU(2) and SU(3) counterparts, which develop Neel and three-sublattice stripe-like long-range order. Since the ground state of a dimer is not a singlet for SU(4) but a 6-dimensional irrep, this leaves the door open for further symmetry breaking. We provide evidence that, unlike in SU(4) ladders, where dimers pair up to form singlet plaquettes, here the SU(4) symmetry is additionally broken, leading to a gapless spectrum in spite of the broken translational symmetry.
Philippe Corboz, Andreas M. Läuchli, Karlo Penc, Matthias Troyer, Frédéric Mila, arXiv:1108.2857
|
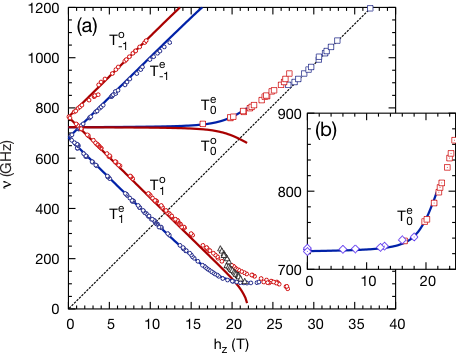 |
Effect of Dzyaloshinskii-Moriya interactions on the phase diagram and magnetic excitations of SrCu2(BO3)2
The orthogonal dimer structure of the SrCu2(BO3)2 spin-1/2 magnet provides a realization of the Shastry-Sutherland model. Using a dimer-product variational wave function, we map out the phase diagram of the Shastry-Sutherland model including anisotropies. Based on the variational solution, we construct a bond-wave approach to obtain the excitation spectra as a function of the magnetic field. The characteristic features of the experimentally measured neutron and ESR spectra are reproduced, like the anisotropy-induced zero-field splittings and the persistent gap at higher fields.
Judit Romhányi, Keisuke Totsuka, Karlo Penc, Phys. Rev. B 83, 024413 (2011).
|
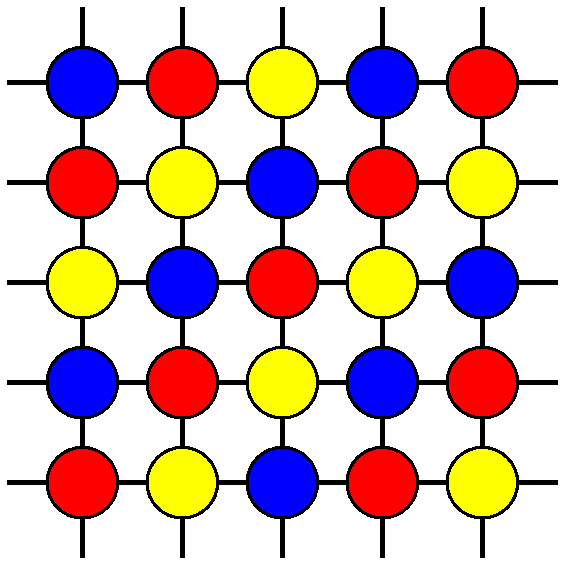 |
Three-Sublattice Ordering of the SU(3) Heisenberg Model of Three-Flavor Fermions on the Square and Cubic Lattices
Combining a semiclassical analysis with exact diagonalizations, we show that the ground state of the SU(3) Heisenberg model on the square lattice develops three-sublattice long-range order. This surprising pattern for a bipartite lattice with only nearest-neighbor interactions is shown to be the consequence of a subtle quantum order-by-disorder mechanism. By contrast, thermal fluctuations favor two-sublattice configurations via entropic selection. These results are shown to extend to the cubic lattice, and experimental implications for the Mott-insulating states of three-flavor fermionic atoms in optical lattices are discussed.
Tamás A. Tóth, Andreas M. Läuchli, Frédéric Mila, Karlo Penc, Phys. Rev. Lett 105, 265301 (2010).
|
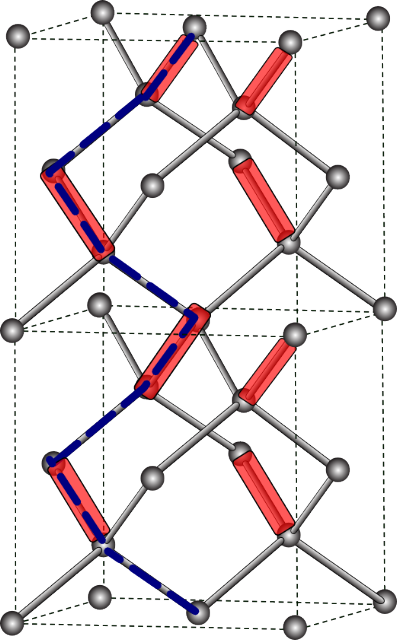 |
A quantum liquid with deconfined fractional excitations in three dimensions
Excitations which carry ``fractional" quantum numbers are known to exist in one dimension in polyacetylene, and in two dimensions, in the fractional quantum Hall effect. Fractional excitations have also been invoked to explain the breakdown of the conventional theory of metals in a wide range of three-dimensional materials. However the existence of fractional excitations in three dimensions remains highly controversial. In this Letter we report direct numerical evidence for the existence of a quantum liquid phase supporting fractional excitations in a concrete, three-dimensional microscopic model - the quantum dimer model on a diamond lattice. We demonstrate explicitly that the energy cost of separating fractional monomer excitations vanishes in this liquid phase, and that its energy spectrum matches that of the Coulomb phase in (3+1) dimensional quantum electrodynamics.
Olga Sikora, Frank Pollman, Nic Shannon, Karlo Penc, Peter Fulde, Phys. Rev. Lett. 103, 247001 (2009)
|